
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$. 分析 由函数的图象的顶点坐标求出A,由周期求出ω,可得f(x)的解析式.根据函数的周期性,求得要求式子的值.
解答 解:根据函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象,
可得A=2,T=$\frac{2π}{ω}$=2(6-2),φ=0,
∴函数f(x)的周期为,8ω=$\frac{π}{4}$.f(x)=2sin$\frac{π}{4}$x.
∵f(1)+f(2)+…+f(8)=$\sqrt{2}$+2+$\sqrt{2}$+0-$\sqrt{2}$-2-$\sqrt{2}$+0=0,
∴f(1)+f(2)+…+f(2017)=252•[f(1)+f(2)+…+f(8)]+f(1)=0+$\sqrt{2}$=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,根据函数的周期性求函数的值,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 14 | B. | 12 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
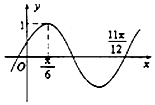 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
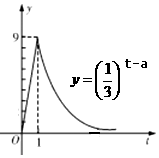 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com