
 �ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��ص���������Ľ��������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ���ϵ׳�Ϊ1���µ׳�Ϊ2�����Σ��ҵ�ʵ��tȡ[0��3]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ����߶γ�����ȣ���ͼ1�����Ϊ��������
�ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��ص���������Ľ��������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ���ϵ׳�Ϊ1���µ׳�Ϊ2�����Σ��ҵ�ʵ��tȡ[0��3]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ����߶γ�����ȣ���ͼ1�����Ϊ��������| A�� | 4 | B�� | $\frac{9}{2}$ | C�� | 5 | D�� | $\frac{11}{2}$ |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
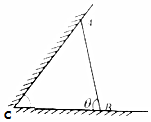 ij����ҪΪ������С���ィ��һ�����濿ǽ��������¶���ң�������״��ͼ��ʾ����֪��������ǽ�ļн�Ϊ$\frac{��}{3}$����ACB=$\frac{��}{3}$����ǽAB�ij���Ϊ6�ף�����������ǽ�Ŀ����ó����㹻���ǡ�ABC=��
ij����ҪΪ������С���ィ��һ�����濿ǽ��������¶���ң�������״��ͼ��ʾ����֪��������ǽ�ļн�Ϊ$\frac{��}{3}$����ACB=$\frac{��}{3}$����ǽAB�ij���Ϊ6�ף�����������ǽ�Ŀ����ó����㹻���ǡ�ABC=���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��D����ֱ��BC�� | B�� | ��D��BC���ӳ����� | ||
| C�� | ��D���߶�BC�� | D�� | ��D��CB���ӳ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��3���� ��4���� | ����a�ͳ� | ����b�ͳ� |
| ����a�ͳ� | 60% | 50% |
| ����b�ͳ� | 40% | 50% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����f��x��=Asin����x+�գ���A��0���أ�0����ͼ����ͼ��ʾ����f��1��+f��2��+f��3��+��+f��2017��=$\sqrt{2}$��
����f��x��=Asin����x+�գ���A��0���أ�0����ͼ����ͼ��ʾ����f��1��+f��2��+f��3��+��+f��2017��=$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com