
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 14 | B. | 12 | C. | 9 | D. | 7 |
分析 利用椭圆的标准方程及其性质、斜率计算公式、两点之间的距离公式即可得出.
解答 解:设Q(x,y),T(x1,y1),S(x2,y2),QA1,QA2斜率分别为k1,k2,
则OT,OS的斜率为k1,k2,且${k_1}{k_2}=\frac{y}{x+3}•\frac{y}{x-3}=\frac{y^2}{{{x^2}-9}}=-\frac{5}{9}$,
所以$O{T^2}={x_1}^2+{y_1}^2={x_1}^2+{k_1}^2{x_1}^2=\frac{{45({1+{k_1}^2})}}{{5+9{k_1}^2}}$,同理$O{S^2}=\frac{{45({1+{k_2}^2})}}{{5+9{k_2}^2}}$,
因此${|{OS}|^2}+{|{OT}|^2}=\frac{{45({1+{k_1}^2})}}{{5+9{k_1}^2}}+\frac{{45({1+{k_2}^2})}}{{5+9{k_2}^2}}=\frac{{45({1+{k_1}^2})}}{{5+9{k_1}^2}}+\frac{{45({1+\frac{25}{{81{k_1}^2}}})}}{{5+\frac{25}{{9{k_1}^2}}}}$=$\frac{{45({1+{k_1}^2})}}{{5+9{k_1}^2}}+\frac{{81{k_1}^2+25}}{{5+9{k_1}^2}}=\frac{{126{k_1}^2+70}}{{5+9{k_1}^2}}=14$.
故选:A.
点评 本题考查了椭圆的定义标准方程及其性质、斜率计算公式、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | 16 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
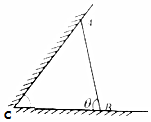 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )| A. | 求24名男生的达标率 | B. | 求24名男生的不达标率 | ||
| C. | 求24名男生的达标人数 | D. | 求24名男生的不达标人数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com