
分析 (1)由2cos2A+3=4cosA,利用倍角公式可得$2co{s^2}A+\frac{1}{2}=2cosA$,化简解出即可得出.
(2)利用正弦定理、和差公式、三角函数的单调性即可得出.
解答 解:(1)因为2cos2A+3=4cosA,所以$2co{s^2}A+\frac{1}{2}=2cosA$,
所以4cos2A-4cosA+1=0,
所以$cosA=\frac{1}{2}$.
又因为0<A<π,所以$A=\frac{π}{3}$.
(2)因为$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,$A=\frac{π}{3}$,a=2,
所以$b=\frac{4}{{\sqrt{3}}}sinB,c=\frac{4}{{\sqrt{3}}}{sinC}$,
所以$l=2+b+c=2+\frac{4}{{\sqrt{3}}}({sinB+{sinC}})$.
因为$B+C=\frac{2π}{3}$,
所以$l=2+\frac{4}{{\sqrt{3}}}[{sinB+sin({\frac{2π}{3}-B})}]=2+sin({B+\frac{π}{6}})$.
又因为$0<B<\frac{2π}{3}$,所以$\frac{1}{2}<sin({B+\frac{π}{6}})≤1$,所以l∈(4,6].
点评 本题考查了倍角公式、正弦定理、和差公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | $\frac{11}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 14 | B. | 12 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
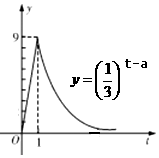 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com