
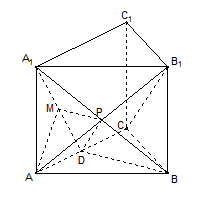
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是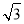 ,D是AC的中点.
,D是AC的中点.

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
(1)详见解析;(2)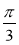 ;(3)
;(3)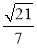 .
.
【解析】
试题分析:(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点,根据中位线定理可知PD∥B1C,
根据线面平行即可得证;(2)由于AA1⊥底面ABC,且BD⊥AC,所以A1D⊥BD,可知∠A1DA就是二面角A1-BD-A的平面角,在三角形A1DA 中,tan∠A1DA=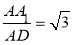 ,即可求出二面角的平面角为
,即可求出二面角的平面角为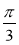 ,即可求出二面角;(3)由(2)作AM⊥A1D,M为垂足,由于BD⊥AC,平面A1ACC1⊥平面ABC,可证BD⊥平面A1ACC1,即可BD⊥AM,可证明AM⊥平面A1DB,连接MP,可知∠APM就是直线A1B与平面A1BD所成的角,在Rt△AA1D中就可以求出∠APM的正弦值,进而求出结果.
,即可求出二面角;(3)由(2)作AM⊥A1D,M为垂足,由于BD⊥AC,平面A1ACC1⊥平面ABC,可证BD⊥平面A1ACC1,即可BD⊥AM,可证明AM⊥平面A1DB,连接MP,可知∠APM就是直线A1B与平面A1BD所成的角,在Rt△AA1D中就可以求出∠APM的正弦值,进而求出结果.
【解析】
(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点,
∵D为AC中点,∴PD∥B1C,
又∵PD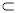 平面A1BD,∴B1C∥平面A1BD;
平面A1BD,∴B1C∥平面A1BD;
(2)∵正三棱住ABC-A1B1C1,∴AA1⊥底面ABC,
又∵BD⊥AC,∴A1D⊥BD,∴∠A1DA就是二面角A1-BD-A的平面角,
∵AA1= ,AD=
,AD=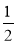 AC=1,∴tan∠A1DA=
AC=1,∴tan∠A1DA=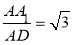 ,∴∠A1DA=
,∴∠A1DA=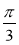 ,即二面角A1-BD-A的大小是
,即二面角A1-BD-A的大小是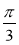 ;
;
(3)由(2)作AM⊥A1D,M为垂足,
∵BD⊥AC,平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,∴BD⊥平面A1ACC1,
∵AM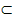 平面A1ACC1,∴BD⊥AM,
平面A1ACC1,∴BD⊥AM,
∵A1D∩BD=D,∴AM⊥平面A1DB,连接MP,
则∠APM就是直线A1B与平面A1BD所成的角,
∵AA1= ,AD=1,∴在Rt△AA1D中,∠A1DA=
,AD=1,∴在Rt△AA1D中,∠A1DA=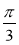 ,∴AM=1×sin60°=
,∴AM=1×sin60°=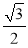 ,AP=
,AP=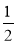 AB1=
AB1=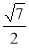 ,∴sin∠APM=
,∴sin∠APM= ,∴直线AB1与平面A1BD所成的角的正弦值为
,∴直线AB1与平面A1BD所成的角的正弦值为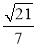 .
.
考点:1.线面平行的判定;2.二面角大小;3线面成角大小.


科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中理科数学试卷(解析版) 题型:填空题
设随机变量的分布列为P(
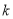 )=
)=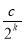 ,(k=1,2,3), 其中c为常数,则E
,(k=1,2,3), 其中c为常数,则E .
.
查看答案和解析>>
科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中理科数学试卷(解析版) 题型:选择题
从5男4女中选4位代表,其中至少有2位男生,且至少有1位女生,分别到四个不同的工厂调查,不同的分派方法有
A、100种 B、400种 C、4800种 D、2400种
查看答案和解析>>
科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中文科数学试卷(解析版) 题型:选择题
已知函数 有两个极值点
有两个极值点 ,若
,若 ,则关于
,则关于 的方程
的方程 的不同实根个数为 ( )
的不同实根个数为 ( )
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com