Question

17．如图，点B是以AC为直径的圆周上的一点，AB=BC，AC=4，PA=AB，PA⊥平面ABC，点E为PB的中点．
（Ⅰ）求证：平面AEC⊥平面PBC；
（Ⅱ）求直线AE与平面PAC所成角的大小．

Answer 1

分析 （Ⅰ）证明BC⊥面PAC，推出BC⊥AE，然后证明AE⊥PB，推出AE⊥平面PBC，然后证明平面AEC⊥平面PBC．
（Ⅱ）作BO⊥平面APC，取PO的中点G，连结EG，连结AG，说明∠EAG就是直线AE与平面PAC所成角，通过解三角形求解即可．

解答 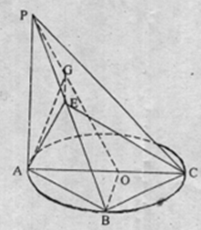证明：（Ⅰ）∵PA⊥⊙O所在平面，且BC为⊙O的弦，
∴PA⊥BC
∵AB为⊙O的直径，
∴BC⊥AC．
而PA∩AC=A．
∴BC⊥面PAC，
∵AE?平面PAC，∴BC⊥AE，
∵PA=AB，PA⊥平面ABC，点E为PB的中点．
∴AE⊥PB，PB∩BC=B，
∴AE⊥平面PBC．
∵AE?平面AEC，
∴平面AEC⊥平面PBC．
（Ⅱ）作BO⊥平面APC，取PO的中点G，连结EG，
则EG∥BO，⇒EG⊥平面PAC，连结AG，
∴∠EAG就是直线AE与平面PAC所成角，
AE=$\frac{1}{2}$PB=2，$GE=\frac{1}{2}OB=1$，
∴sin∠EAG=$\frac{GE}{AE}$=$\frac{1}{2}$，
∴直线AE与平面PAC所成角为：$\frac{π}{6}$．

点评 本题考查的知识点是直线与平面垂直的判定，直线与平面所成角的求法，其中熟练掌握空间线面垂直、平行的判定、性质，善于根据直角三角形、圆周角的性质，判断出直线与直线垂直是解答本题的关键．