
分析 (Ⅰ)△ABC中,利用三角恒等变换化简条件求得tanA的值,可得A的值.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,求得g(x)的解析式,再利用g(x)的周期求得ω,可得f(x)的解析式,再利用正弦函数的定义域和值域,求得函数f(x)的值域.
解答 解:(Ⅰ)△ABC中,∵$asinB+\sqrt{3}acosB=\sqrt{3}c$,
∴$sinAsinB+\sqrt{3}sinAcosB=\sqrt{3}sinC$,∵C=π-(A+B),
∴$sinAsinB+\sqrt{3}sinAcosB=\sqrt{3}sin(A+B)$=$\sqrt{3}(sinAcosB+cosAsinB)$,
∴$tanA=\sqrt{3}$,∵0<A<π,∴$A=\frac{π}{3}$.
(Ⅱ)由(Ⅰ)得:$f(x)=λ{cos^2}(ωx+\frac{π}{6})-3=λ\frac{{1+cos(2ωx+\frac{π}{3})}}{2}-3$=$\frac{λ}{2}cos(2ωx+\frac{π}{3})+\frac{λ}{2}-3$,
∴λ-3=2,从而λ=5,
∴$f(x)=5{cos^2}(ωx+\frac{π}{6})-3=\frac{5}{2}cos(2ωx+\frac{π}{3})-\frac{1}{2}$,
从而$g(x)=\frac{5}{2}cos(\frac{4}{3}ωx+\frac{π}{3})-\frac{1}{2}$,
∴$\frac{2π}{{\frac{4}{3}ω}}=π⇒ω=\frac{3}{2}$,∴$f(x)=\frac{5}{2}cos(3x+\frac{π}{3})-\frac{1}{2}$.
当$x∈[0,\frac{π}{2}]$时,$\frac{π}{3}≤3x+\frac{π}{3}≤\frac{11}{6}π$,
∴$-1≤cos(3x+\frac{π}{3})≤\frac{{\sqrt{3}}}{2}$,
从而$-3≤f(x)≤\frac{{5\sqrt{3}-2}}{4}$,
∴f(x)的值域为$[-3,\frac{{5\sqrt{3}-2}}{4}]$.
点评 本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
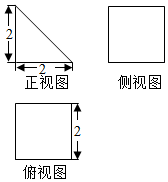 如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )
如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
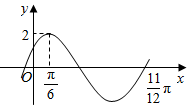 函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax${\;}_{0}^{2}$-bx0 | B. | ?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax${\;}_{0}^{2}$-bx0 | ||
| C. | ?x∈R,$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax${\;}_{0}^{2}$-bx0 | D. | ?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax${\;}_{0}^{2}$-bx0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com