Question

在三棱锥P-ABC中，PA=BC=2

34

，PB=AC=10，PC=AB=2

41

，则三棱锥P-ABC的体积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：构造长方体AQPS-MBNC，以S为原点，SA为x轴，SP为y轴，SC为z轴，建立空间直角坐标系，利用向量法能求出三棱锥P-ABC的体积．

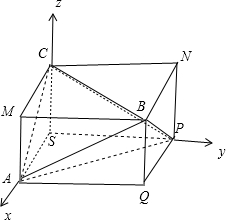
解答： 解：如图，构造长方体AQPS-MBNC，
以S为原点，SA为x轴，SP为y轴，SC为z轴，
建立空间直角坐标系，
设SA=a，SP=b，SC=c，
∵PA=BC=2

34

，PB=AC=10，PC=AB=2

41

，
∴

a2+b2=136 a2+c2=100 b2+c2=164

，解得a=6，b=10，c=8，
A（6，0，0），B（6，10，8），C（0，0，8），P（0，10，0），
∴

AC

=（-6，0，8），

AB

=（0，10，8），

BP

=（-6，0，-8）
cos＜

AB

，

AC

＞=

64

10×2 41

=

16

5 41

，∴sin＜

AB

，

AC

＞=

769

5 41

，
∴S_△ABC=

1

2

×|AB|×|AC|×sin＜

AB

•

AC

＞
=

1

2

×2

41

×10×

769

5 41

=2

769

．
设平面ABC的法向量

n

=(x，y，z)，

n • AB =10y+8z=0 n • AC =-6x+8z=0

，取x=20，得

n

=（20，-12，15），
∴P到平面ABC的距离：
d=

| BP • n |

| n |

=

|-120-120|

400+144+225

=

240

769

，
∴三棱锥P-ABC的体积：
V=

1

3

×S△ABC×d=

1

3

×2

769

×

240

769

=160．
故答案为：160．

点评：本题考查三棱锥的体积的求法，解题时要认真审题，注意构造法和向量法的合理运用．