
分析 (Ⅰ)$f'(x)=\frac{1}{x}$,$F'(x)=1-\frac{2}{x^2}$.由函数f(x)与F(x)有公共切线,知函数f(x)与F(x)的图象相切或无交点.由此能求出a的取值范围.
(Ⅱ)等价于xlnx+a+e-2-ax≥0在x∈(0,+∞)上恒成立,令g(x)=xlnx+a+e-2-ax,g'(x)=lnx+1-a,令g'(x)=0,得$x=\frac{e^a}{e}$,从而求出g(x)的最小值,令$t(x)=x+e-2-\frac{e^x}{e}$,由$t'(x)=1-\frac{e^x}{e}$=0,得x=1,由此能求出a的取值范围.
解答 解:(Ⅰ)$f'(x)=\frac{1}{x}$,$F'(x)=1-\frac{2}{x^2}$.
∵函数f(x)与F(x)有公共切线,∴函数f(x)与F(x)的图象相切或无交点.
当两函数图象相切时,设切点的横坐标为x0(x0>0),则$f'({x_0})=\frac{1}{x_0}=F'({x_0})=1-\frac{2}{{{x_0}^2}}$,
解得x0=2或x0=-1(舍去),
则f(2)=F(2),得a=ln2-3,
由此求出a≥ln2-3,即a的取值范围为[ln2-3,+∞).
(Ⅱ)等价于xlnx+a+e-2-ax≥0在x∈(0,+∞)上恒成立,
令g(x)=xlnx+a+e-2-ax,
因为g'(x)=lnx+1-a,令g'(x)=0,得$x=\frac{e^a}{e}$,
| x | $(0,\frac{e^a}{e})$ | $\frac{e^a}{e}$ | $(\frac{e^a}{e},+∞)$ |
| g'(x) | - | 0 | + |
| g(x) | 极小值 |
| x | (0,1) | 1 | (1,+∞) |
| t'(x) | + | 0 | - |
| t(x) | 极大值 |
点评 本题考查实数的取值范围、导数性质、构造法、导数的几何意义等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想、分类与整合思想,考查创新意识、应用意识,是中档题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
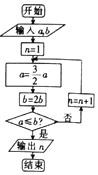 名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )
名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com