
分析 根据双曲线x2-$\frac{{y}^{2}}{9}$=1求出左右焦点坐标,$\overrightarrow{PM}•\overrightarrow{PN}$=0,说明∠MPN=90°,△MNP是直角三角形,利用双曲线的定义即可求解.
解答 解:由题意:双曲线x2-$\frac{{y}^{2}}{9}$=1,
可得:a=1.b=3,c=$\sqrt{10}$
M,N分别为双曲线x2-$\frac{{y}^{2}}{9}$=1的左右焦点,
∴M(-$\sqrt{10}$,0),N($\sqrt{10}$,0),|MN|=2$\sqrt{10}$.
又∵P在双曲线上,且$\overrightarrow{PM}•\overrightarrow{PN}$=0,
∴∠MPN=90°,△MNP是直角三角形.
设|NP|=m,|MP|=n,
m2+n2=(2c)2=40,
根据双曲线的定义可得|m-n|=2a=2.
则有(m-n)2=4,
解得:mn=18,
所以:|$\overrightarrow{PM}$|+|$\overrightarrow{PN}$|=m+n=$\sqrt{(m-n)^{2}+4mn}$=2$\sqrt{19}$.
故答案为$2\sqrt{19}$.
点评 本题主要考查了双曲线的定义和简单性质的运用能力.属于基础题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
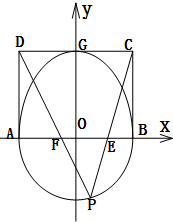 已知曲线C的图形如图所示,其上半部分是半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$,下半部分是半圆x2+y2=b2(y≤0),(a>b>0),半椭圆内切于矩形ABCD,且CD交y轴于点G,点P是半圆上异于A,B的任意一点,当点P位于点$M(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{3}}}{3})$时,△AGP的面积最大.
已知曲线C的图形如图所示,其上半部分是半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$,下半部分是半圆x2+y2=b2(y≤0),(a>b>0),半椭圆内切于矩形ABCD,且CD交y轴于点G,点P是半圆上异于A,B的任意一点,当点P位于点$M(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{3}}}{3})$时,△AGP的面积最大.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | 39 | 49 | 58 |
| A. | 111.9万元 | B. | 112.1万元 | C. | 113.7万元 | D. | 113.9万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com