
已知函数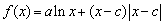 ,
,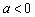 ,
,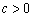 .
.
(1)当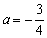 ,
,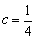 时,求函数
时,求函数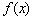 的单调区间;
的单调区间;
(2)当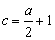 时,若
时,若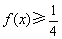 对
对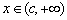 恒成立,求实数
恒成立,求实数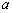 的取值范围;
的取值范围;
(3)设函数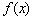 的图象在点
的图象在点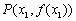 、
、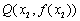 两处的切线分别为
两处的切线分别为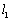 、
、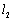 .若
.若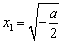 ,
,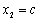 ,且
,且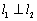 ,求实数
,求实数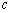 的最小值.
的最小值.
解:函数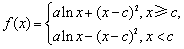 ,求导得
,求导得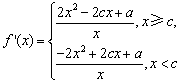 .
.
(1)当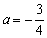 ,
,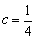 时,
时,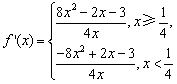 ,
,
若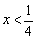 ,则
,则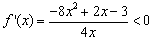 恒成立,
恒成立, 所以
所以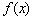 在
在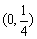 上单调减;
上单调减;
若 ,则
,则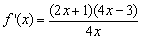 ,令
,令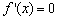 ,解得
,解得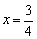 或
或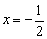 (舍),
(舍),
当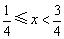 时,
时,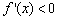 ,
,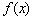 在
在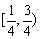 上单调减;
上单调减;
当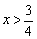 时,
时,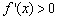 ,
,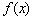 在
在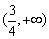 上单调增.
上单调增.
所以函数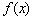 的单调减区间是
的单调减区间是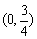 ,单调增区间是
,单调增区间是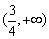 . ………………4分
. ………………4分
(2)当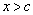 ,
,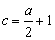 时,
时,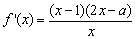 ,而
,而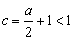 ,所以
,所以
当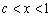 时,
时,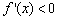 ,
,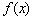 在
在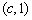 上单调减;
上单调减;
当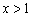 时,
时,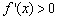 ,
,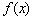 在
在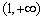 上单调增.
上单调增.
所以函数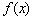 在
在 上的最小值为
上的最小值为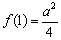 ,
,
所以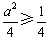 恒成立,解得
恒成立,解得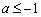 或
或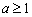 ,
,
又由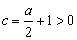 ,得
,得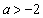 ,所以实数
,所以实数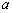 的取值范围是
的取值范围是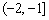 . ……………9分
. ……………9分
(3)由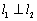 知,
知,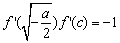 ,而
,而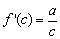 ,则
,则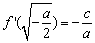 ,
,
若 ,则
,则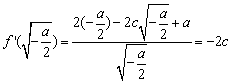 ,所以
,所以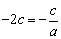 ,
,
解得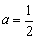 ,不符合题意; ……………………………11分
,不符合题意; ……………………………11分
故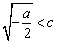 ,则
,则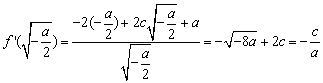 ,
,
整理得,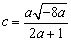 ,由
,由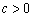 得,
得,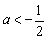 , …………………………13分
, …………………………13分
令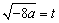 ,则
,则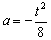 ,
,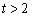 ,所以
,所以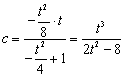 ,
,
设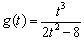 ,则
,则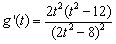 ,
,
当 时,
时,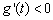 ,
,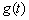 在
在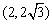 上单调减;
上单调减;
当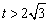 时,
时, ,
,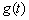 在
在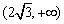 上单调增.
上单调增.
所以,函数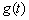 的最小值为
的最小值为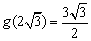 ,故实数
,故实数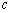 的最小值为
的最小值为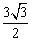 . ……16分
. ……16分


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
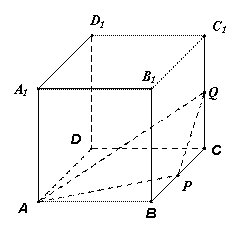
正方体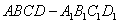 为棱长为1,动点
为棱长为1,动点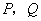 分别在棱
分别在棱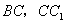 上,过点
上,过点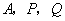 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为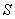 ,设
,设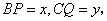 其中
其中 ,下列命题正确的是
,下列命题正确的是
(写出所有正确命题的编号)
①当 时,
时,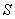 为矩形,其面积最大为1;
为矩形,其面积最大为1;
②当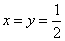 时,
时,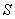 为等腰梯形;
为等腰梯形;
③当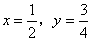 时,
时,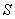 为六边形;
为六边形;
④当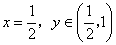 时,设
时,设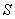 与棱
与棱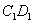 的交点为
的交点为 ,则
,则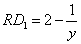
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).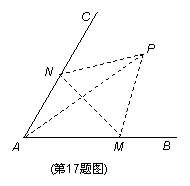
查看答案和解析>>
科目:高中数学 来源: 题型:
徐州古称彭城,三面环山,历来是兵家必争之地,拥有云龙山、户部山、子房山和九里山等四大名山.一位游客来徐州游览,已知该游客游览云龙山的概率为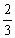 ,游览户部山、子房山和九里山的概率都是
,游览户部山、子房山和九里山的概率都是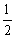 ,且该游客是否游览这四座山相互独立.
,且该游客是否游览这四座山相互独立.
(1)求该游客至多游览一座 山的概率;
山的概率;
(2)用随机变量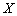 表示
表示 该游客游览的山数,求
该游客游览的山数,求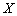 的概率分布和数学期望
的概率分布和数学期望 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com