
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).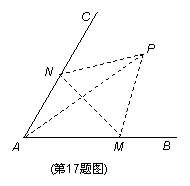
解法一:设∠AMN=θ,在△AMN中,
因为MN=2,所以AM= sin(120°-θ) . ………………2分
sin(120°-θ) . ………………2分
在△APM中,cos∠AMP=cos(60°+θ). …………………6分
AP2=AM2+MP2-2 AM·MP·cos∠AMP
= sin2(120°-θ)+4-2×2×
sin2(120°-θ)+4-2×2× sin(120°-θ) cos(60°+θ) ………………………………8分
sin(120°-θ) cos(60°+θ) ………………………………8分
= sin2(θ+60°)-
sin2(θ+60°)- sin(θ+60°) cos(θ+60°)+4
sin(θ+60°) cos(θ+60°)+4
=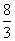 [1-cos (2θ+120°)]-
[1-cos (2θ+120°)]- sin(2θ+120°)+4
sin(2θ+120°)+4
=-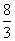 [
[ sin(2θ+120°)+cos (2θ+120°)]+
sin(2θ+120°)+cos (2θ+120°)]+
= -
- sin(2θ+150°),θ∈(0,120°).
sin(2θ+150°),θ∈(0,120°).
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2 .
.
答:设计∠AMN为60时,工厂产生的噪声对居民的影响最小.
 解法二(构造直角三角形):
解法二(构造直角三角形):
设∠PMD=θ,在△PMD中,
∵PM=2,∴PD=2sinθ,MD=2cosθ. ……………2分
在△AMN中,∠ANM=∠PMD=θ,∴ =
= ,
,
AM= sinθ,∴AD=
sinθ,∴AD= sinθ+2cosθ,(θ≥
sinθ+2cosθ,(θ≥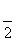 时,结论也正确).……………6分
时,结论也正确).……………6分
AP2=AD2+PD2=( sinθ+2cosθ)2+(2sinθ)2
sinθ+2cosθ)2+(2sinθ)2
= sin2θ+
sin2θ+ sinθcosθ+4cos2θ+4sin2θ
sinθcosθ+4cos2θ+4sin2θ
= ·
· +
+ sin2θ+4=
sin2θ+4= sin2θ-
sin2θ-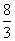 cos2θ+
cos2θ+
 此时AM=AN=2,∠PAB=30°
此时AM=AN=2,∠PAB=30°
解法三:设AM=x,AN=y,∠AMN=α.
在△AMN中,因为MN=2,∠MAN=60°,
所以MN2=AM2+AN2-2 AM·AN·cos∠MAN,
即x2+y2-2xycos60°=x2+y2-xy=4.
 因为x2+y2-xy=4,4+xy=x2+y2≥2xy,即xy≤4.
因为x2+y2-xy=4,4+xy=x2+y2≥2xy,即xy≤4.
所以AP2≤12,即AP≤2 .
.
当且仅当x=y=2时,AP取得最大值2 .
.
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小.
解法四(坐标法):以AB所在的直线为x轴,A为坐标原点,建立直角坐标系.
设M(x1,0),N(x2, x2),P(x0,y0).∵MN=2,
x2),P(x0,y0).∵MN=2,
∴(x1-x2)2+3x =4.
=4.
 =4+4x1x2≤4+4×2=12, 即AP≤2
=4+4x1x2≤4+4×2=12, 即AP≤2 .
.
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小. 解法五(变换法):以AB所在的直线为x轴,A为坐标原点,建立直角坐标系.
 设M(x1,0),N(x2,
设M(x1,0),N(x2, x2),P(x0,y0).
x2),P(x0,y0).
∵MN=2,∴(x1-x2)2+3x =4.即x
=4.即x +4x
+4x =4+2x1x2
=4+2x1x2
∴4+2x1x2≥4x1x2,即x1x2≤2. …………………4分
∵△MNP为正三角形,且MN=2.∴PK= ,PK⊥MN.
,PK⊥MN.
 x0-x1=
x0-x1=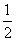 (x2-x1)+
(x2-x1)+ x2,y0=-
x2,y0=- (x2-x1)+
(x2-x1)+ x2.
x2.
∴x0=2x2+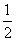 x1,y0=
x1,y0= x1.
x1.
∴AP2=x +y
+y =(2x2+
=(2x2+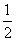 x1)2+
x1)2+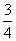 x
x =x
=x +4x
+4x +2x1x2
+2x1x2
=4+4x1x2≤4+4×2=12, 即AP≤2 .
.
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小.…
 解法六(几何法):由运动的相对性,可使△PMN不动,点A在运动.
解法六(几何法):由运动的相对性,可使△PMN不动,点A在运动.
由于∠MAN=60°,∴点A在以MN为弦的一段圆弧(优弧)上,
设圆弧所在的圆的圆心为F,半径为R,
由图形的几何性质知:AP的最大值为PF+R.
在△AMN中,由正弦定理知: =2R,
=2R,
∴R= ,
,
∴FM=FN=R= ,又PM=PN,∴PF是线段MN的垂直平分线.
,又PM=PN,∴PF是线段MN的垂直平分线.
设PF与MN交于E,则FE2=FM2-ME2=R2-12= .
.
即FE= ,又PE=
,又PE= .
.
∴PF= ,∴AP的最大值为PF+R=2
,∴AP的最大值为PF+R=2 .
.
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),且.若直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,则实数k的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数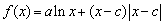 ,
,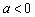 ,
,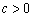 .
.
(1)当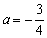 ,
,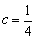 时,求函数
时,求函数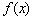 的单调区间;
的单调区间;
(2)当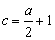 时,若
时,若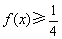 对
对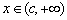 恒成立,求实数
恒成立,求实数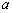 的取值范围;
的取值范围;
(3)设函数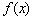 的图象在点
的图象在点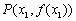 、
、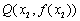 两处的切线分别为
两处的切线分别为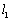 、
、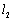 .若
.若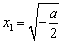 ,
,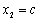 ,且
,且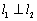 ,求实数
,求实数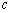 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com