已知函数f(x)=ax+lnx(a∈R)
(1)求f(x)的单调区间;
(2)设g(x)=x2-2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求实数a的取值范围.
解:(1)

…(2分)
当a≥0时,由于x∈(0,+∞),f′(x)>0,所以函数f(x)的单调增区间为(0,+∞),…(4分)
当a<0时,令f'(x)=0,得
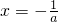
.
当x变化时,f'(x)与f(x)变化情况如下表:

所以函数f(x)的单调增区间为(0,
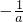
),函数f(x)的单调减区间为
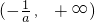
…(6分)
(2)由已知,转化为f(x)
max<g(x)
max…(8分)
因为g(x)=x
2-2x+2=(x-1)
2+1,x∈[0,1],
所以g(x)
max=2…(9分)
由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.
(或者举出反例:存在f(e
3)=ae
3+3>2,故不符合题意.) …(10分)
当a<0时,f(x)在
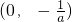
上单调递增,在
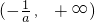
上单调递减,
故f(x)的极大值即为最大值,

,…(11分)
所以2>-1-ln(-a),解得

.…(12分)
分析:(1)先求f(x)的导数,再对参数a进行讨论,利用导数函数值的正负,从而可求f(x)的单调区间;
(2)对任意x
1∈(0,+∞),均存在x
2∈[0,1],使得f(x
1)<g(x
2),等价于f(x)
max<g(x)
max,分别求出相应的最大值,即可求得实数a的取值范围.
点评:本题重点考查导数知识的运用,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,解题的关键是利用导数确定函数的单调性

 …(2分)
…(2分)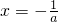 .
.
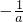 ),函数f(x)的单调减区间为
),函数f(x)的单调减区间为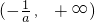 …(6分)
…(6分)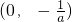 上单调递增,在
上单调递增,在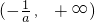 上单调递减,
上单调递减, ,…(11分)
,…(11分) .…(12分)
.…(12分)

 名校课堂系列答案
名校课堂系列答案