
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的一点.
上的一点.

(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1) 根据三棱柱是直三棱柱的特征,又![]() ,可作
,可作![]() 中点
中点![]() ,连接DM,通过线面垂直证明
,连接DM,通过线面垂直证明![]() 平面
平面![]() ,可推出
,可推出![]() ,又
,又![]() ,可证
,可证![]()
(2) 通过作图,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角体系,先通过几何法求出
轴,建立空间直角体系,先通过几何法求出![]() 长度,分别表示出线面角各点对应的坐标,再用向量公式算出直线
长度,分别表示出线面角各点对应的坐标,再用向量公式算出直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
证明:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,有
,有![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为三棱柱![]() 为直三棱柱,
为直三棱柱,
所以平面![]() 平面
平面![]() ,
,
又因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]()
又因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() .
.
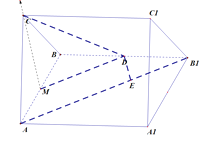
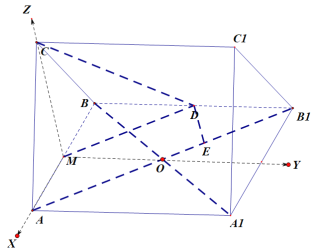
(2)设![]() ,如图以
,如图以![]() 为坐标原点,
为坐标原点,
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角体系,
轴,建立空间直角体系,
由(1)可知![]() ,
,![]() ,所以
,所以![]() ,
,
故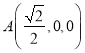 ,
,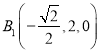 ,
,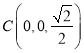 ,
,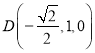 ,
,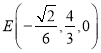 ,
,
对平面![]() ,
,![]() ,
,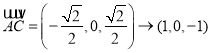 ,
,
所以其法向量可表示为![]() .
.
又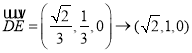 ,
,
所以直线![]() 与平面
与平面![]() 成角的正弦值
成角的正弦值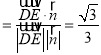 .
.![]()


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险第一年的费用(基准保费)统一为
座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表(其中浮动比率是在基准保费上上下浮动):
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表(其中浮动比率是在基准保费上上下浮动):
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
某机构为了研究某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
(Ⅰ)求这![]() 辆车普通
辆车普通![]() 座以下私家车在第四年续保时保费的平均值(精确到
座以下私家车在第四年续保时保费的平均值(精确到![]() 元)
元)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基准保费的车辆记为事故车.假设购进一辆事故车亏损![]() 元,一辆非事故车盈利
元,一辆非事故车盈利![]() 元,且各种投保类型车的频率与上述机构调查的频率一致.试完成下列问题:
元,且各种投保类型车的频率与上述机构调查的频率一致.试完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在该店内随机挑选![]() 辆车,求这
辆车,求这![]() 辆车恰好有一辆为事故车的概率;
辆车恰好有一辆为事故车的概率;
②若该销售商一次购进![]() 辆车(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
辆车(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到两焦点
上任意一点到两焦点![]() 距离之和为
距离之和为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆C交于
与椭圆C交于![]() 两点.点
两点.点![]() 为椭圆上一点,求
为椭圆上一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,底面ABFE是边长为2的正方形,DE与CF均垂直于平面ABFE,且![]() .
.
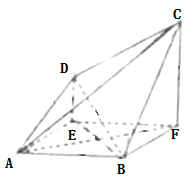
(1)证明:BE∥平面ACD;
(2)求三棱锥B﹣ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 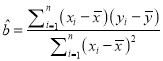
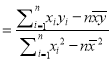 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△OAB中,顶点A的坐标是(3,0),顶点B的坐标是(1,2),记△OAB位于直线![]() 左侧图形的面积为f(t).
左侧图形的面积为f(t).

(1)求函数f(t)的解析式;
(2)设函数![]() ,求函数
,求函数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com