
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 是
是![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上.
上.
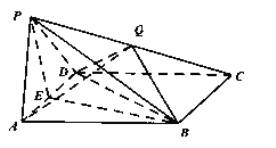
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(3)若![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由线面垂直判定定理,要证线面垂直,需证![]() 垂直平面
垂直平面![]() 内两条相交直线,由
内两条相交直线,由![]() ,
,![]() 是
是![]() 的中点,易得
的中点,易得![]() 垂直于
垂直于![]() ,再由底面
,再由底面![]() 是菱形,
是菱形,![]() 得三角形
得三角形![]() 为正三角形,所以
为正三角形,所以![]() 垂直于
垂直于![]() ,(2)由线面平行判定定理,要证线面平行,需证
,(2)由线面平行判定定理,要证线面平行,需证![]() 平行于平面
平行于平面![]() 内一条直线,根据
内一条直线,根据![]() 是
是![]() 的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求
的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求![]() 的值就转化为求对应高的长度比.
的值就转化为求对应高的长度比.
试题解析:(1)因为E是AD的中点,PA=PD,所以AD⊥PE.
因为底面ABCD是菱形,∠BAD=![]() ,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
因为PE∩BE=E,所以AD⊥平面PBE. 4分
(2)连接AC交BD于点O,连结OQ.因为O是AC中点,
Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA. 7分
因为PA![]() 平面BDQ,OQ
平面BDQ,OQ![]() 平面BDQ.所以PA//平面BDQ. 9分
平面BDQ.所以PA//平面BDQ. 9分
(3)设四棱锥P-BCDE,Q-ABCD的分别为![]() ,
,![]() ,所以VP-BCDE=
,所以VP-BCDE=![]() SBCDE
SBCDE![]() ,VQ-ABCD=
,VQ-ABCD=![]() SABCD
SABCD![]() . 10分
. 10分
因为VP-BCDE=2VQ-ABCD,且底面积SBCDE=![]() SABCD. 12分
SABCD. 12分
所以![]() ,因为
,因为![]() ,所以
,所以![]() . 14分
. 14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,
,![]() 为平面上的动点,过点
为平面上的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为直线
为直线![]() 上一点,且满足
上一点,且满足![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和定点
和定点![]() ,其中点
,其中点![]() 是该圆的圆心,
是该圆的圆心,![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求动点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)设曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 是曲线
是曲线![]() 上异于
上异于![]() 的任意一点,记直线
的任意一点,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .证明:
.证明:![]() 是定值;
是定值;
(3)设点![]() 是曲线
是曲线![]() 上另一个异于
上另一个异于![]() 的点,且直线
的点,且直线![]() 与
与![]() 的斜率满足
的斜率满足![]() ,试探究:直线
,试探究:直线![]() 是否经过定点?如果是,求出该定点,如果不是,请说明理由.
是否经过定点?如果是,求出该定点,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且方程
,且方程![]() 有两个相等的实数根
有两个相等的实数根
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 是
是![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() ,求
,求![]() 的解析式;
的解析式;
(3)若不等式![]() 对一切实数
对一切实数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中恰有1名男生的概率是多少?
(3)是否有![]() 把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 与定点
与定点![]() ,
, ![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设曲线![]() 与
与![]() 轴正半轴交点为
轴正半轴交点为![]() ,不经过点
,不经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() ,若
,若![]() .证明:直线
.证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(3)求函数![]() 在定义域上的最大值及最小值,并求出函数取最值时
在定义域上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com