
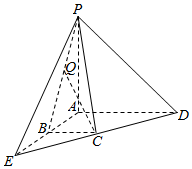
 如图,PA⊥平面ADE,B,C分别是AE,DE的中点,AE⊥AD,AD=AE=AP=2.
如图,PA⊥平面ADE,B,C分别是AE,DE的中点,AE⊥AD,AD=AE=AP=2.分析 以{$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AP}$}为正交基底建立空间直角坐标系Axyz,由题意可得B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2)
(Ⅰ)易得$\overrightarrow{AD}$=(0,2,0)是平面PAB的一个法向量,待定系数可求平面PED的法向量为$\overrightarrow{m}$坐标,由向量的夹角公式可得;
(Ⅱ)设$\overrightarrow{BQ}$=λ$\overrightarrow{BP}$=(-λ,0,2λ)(0≤λ≤1),由夹角公式和二次函数的值域以及余弦函数的单调性可得.
解答 解:以{$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AP}$}为正交基底建立空间直角坐标系Axyz,
则各点的坐标为B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2)
(Ⅰ)∵AD⊥平面PAB,∴$\overrightarrow{AD}$是平面PAB的一个法向量,$\overrightarrow{AD}$=(0,2,0).
∵$\overrightarrow{PC}$=(1,1,-2),$\overrightarrow{PD}$=(0,2,-2).设平面PED的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{m}$•$\overrightarrow{PC}$=0,$\overrightarrow{m}$•$\overrightarrow{PD}$=0,即$\left\{\begin{array}{l}x+y-2z=0\\ 2y-2z=0.\end{array}\right.$,令y=1,解得z=1,x=1.
∴$\overrightarrow{m}$=(1,1,1)是平面PCD的一个法向量,
计算可得cos<$\overrightarrow{AD}$,$\overrightarrow{m}$>=$\frac{\overrightarrow{AD}•m}{|\overrightarrow{AD}||m|}$=$\frac{\sqrt{3}}{3}$,
∴二面角A-PE-D的余弦值为$\frac{\sqrt{3}}{3}$;
(Ⅱ)∵$\overrightarrow{BP}$=(-1,0,2),设$\overrightarrow{BQ}$=λ$\overrightarrow{BP}$=(-λ,0,2λ)(0≤λ≤1),
又$\overrightarrow{CB}$=(0,-1,0),则$\overrightarrow{CQ}$=$\overrightarrow{CB}$+$\overrightarrow{BQ}$=(-λ,-1,2λ),又$\overrightarrow{DP}$=(0,-2,2),
∴cos<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>=$\frac{\overrightarrow{CQ}•\overrightarrow{DP}}{|\overrightarrow{CQ}||\overrightarrow{DP}|}$=$\frac{1+2λ}{\sqrt{10λ^2+2}}$,设1+2λ=t,t∈[1,3],
则cos2<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>=$\frac{2{t}^{2}}{5{t}^{2}-10t+9}$=$\frac{2}{9(\frac{1}{t}-\frac{5}{9})^{2}+\frac{20}{9}}$≤$\frac{9}{10}$,
当且仅当t=$\frac{9}{5}$,即λ=$\frac{2}{5}$时,|cos<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>|的最大值为$\frac{3\sqrt{10}}{10}$.
因为y=cosx在(0,$\frac{π}{2}$)上是减函数,此时直线CQ与DP所成角取得最小值,
又∵BP=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,∴BQ=$\frac{2}{5}$BP=$\frac{2\sqrt{5}}{5}$
点评 本题考查向量法解决立体几何问题,建系并把问题转化为向量的夹角和模长是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{13}$ | B. | $\frac{13}{2}$ | C. | $\frac{2}{17}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0,3) | B. | (0,0,-3) | C. | (0,0,-6) | D. | (0,0,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 |
| [100,110) | 5 |
| [110,120) | 35 |
| [120,130) | 30 |
| [130,140) | 20 |
| [140,150) | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com