
| A. | 121种 | B. | 141种 | C. | 231种 | D. | 282种 |
分析 星期一和星期天的体重相同,所以从这周的第二天开始的中间“减少0.5kg”或“增加0.5kg”的天数必须相同,都是0、1、2、3天,共四种情况,利用组合知识可得结论
解答 解:星期一和星期天的体重相同,所以从这周的第二天开始的中间“减少0.5kg”或“增加0.5kg”的天数必须相同,都是0、1、2、3天,共四种情况
当为0天时,故有${C}_{6}^{0}$=1种,
当有1天时,故有${C}_{6}^{1}•{C}_{5}^{1}$=30种,
当有2天时,故有${C}_{6}^{2}•{C}_{4}^{2}$=90种,
当有3天时,故有${C}_{6}^{3}•{C}_{3}^{3}$=20,
根据分类计数原理可得,1+30+09+20=141种,
故选:B.
点评 本题考查组合知识的运用,考查学生分析解决问题的能力,确定中间“减少0.5kg”或“增加0.5kg”的天数必须相同是关键


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
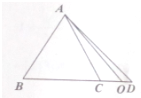 如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).
如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{π}{3},0)$ | B. | $(-\frac{π}{6},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{4},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,a⊥α,则a∥β | |
| B. | 若a,b与α所成的角相等,则a与b平行或相交 | |
| C. | 若α内有三个不共线的点到β的距离相等,则α∥β | |
| D. | 若α∩β=b,a?α且a∥β,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({kπ-\frac{π}{2},kπ})({k∈Z})$ | B. | $({kπ,kπ+\frac{π}{2}})({k∈Z})$ | C. | $({kπ-\frac{π}{4},kπ+\frac{π}{4}})({k∈Z})$ | D. | $({kπ+\frac{π}{4},kπ+\frac{3}{4}π})({k∈Z})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com