
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 方法一:直接观察,归纳可得结论,
方法二,求出数列的前n项和,即可求出n.
解答 解:方法一:$1+\frac{1}{1+2}=\frac{4}{3}$=$\frac{2×2}{2+1}$,
$1+\frac{1}{1+2}+\frac{1}{1+2+3}=\frac{3}{2}$=$\frac{6}{4}$=$\frac{2×3}{3+1}$,
$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}=\frac{8}{5}$=$\frac{2×4}{4+1}$
…,
若$1+\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}+…+\frac{1}{1+2+3+…+n}=\frac{12}{7}$=$\frac{2×6}{6+1}$,
∴n=6,
方法二:$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+n}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{2}{n+1}$)=$\frac{2n}{n+1}$,
令$\frac{2n}{n+1}$=$\frac{12}{7}$,
解得n=6
故选:B
点评 本题考查了归纳推理的问题,关键是找到规律,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
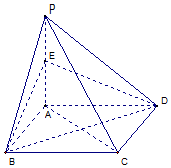 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 142 | B. | 71 | C. | 214 | D. | 107 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
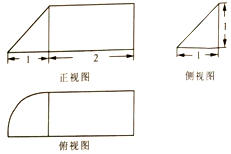
| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com