
分析 (1)由已知点的坐标求得$\overrightarrow{AB}$的坐标,结合$\overrightarrow a∥\overrightarrow{AB}$,且$|{\overrightarrow{AB}}|=\sqrt{5}|{\overrightarrow{OA}}|$列式求出t值,进一步求得cosθ,则向量$\overrightarrow{OB}$的坐标可求;
(2)由$\overrightarrow a$⊥$\overrightarrow{AB}$,把t用cosθ表示,代入$y={cos^2}θ-cosθ+{(\frac{t}{4})^2}$后整理,利用配方法求得最小值.
解答 解:(1)由已知得$\overrightarrow{AB}$=(cosθ-1,t),又$\overrightarrow{a}$∥$\overrightarrow{AB}$,∴2t-cosθ+1=0,
∴cosθ-1=2t.①
又∵|$\overrightarrow{AB}$|=$\sqrt{5}|{\overrightarrow{OA}}|$,∴(cosθ-1)2+t2=5.②
由①②得,5t2=5,∴t2=1.即t=±1.
当t=1时,cosθ=3(舍去),
当t=-1时,cosθ=-1,
∴B(-1,-1),则$\overrightarrow{OB}$=(-1,-1);
(2)由$\overrightarrow a$⊥$\overrightarrow{AB}$可知t=2-2cosθ,
∴y=cos2θ-cosθ+$\frac{{{{(cosθ-1)}^2}}}{4}$=$\frac{5}{4}co{s}^{2}θ-\frac{3}{2}cosθ+\frac{1}{4}$
=$\frac{5}{4}(cosθ-\frac{3}{5})^{2}-\frac{1}{5}$,
∴当cos$θ=\frac{3}{5}$时,${y}_{min}=-\frac{1}{5}$.
点评 本题考查数量积判断两个平面向量的垂直关系,考查了三角函数的化简与求值,考查计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 44 kg | B. | 46 kg | C. | 50 kg | D. | 54 kg |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{12}{13},5)$ | B. | $(-\frac{12}{13},-\frac{5}{13})$ | ||
| C. | $(\frac{12}{13},\frac{5}{13})$或$(-\frac{12}{13},-\frac{5}{13})$ | D. | $(±\frac{12}{13},±\frac{5}{13})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
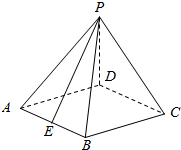 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com