
已知a为实数,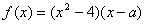 .
.
(1) 求导数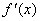 ;
;
(2) 若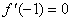 ,求
,求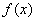 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
(3) 若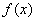 在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
科目:高中数学 来源: 题型:
下列说法错误的是( ).
A.如果命题“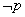 ”与命题“
”与命题“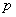 或
或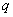 ”都是真命题,那么命题
”都是真命题,那么命题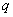 一定是真命题.
一定是真命题.
B. 命题“若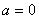 ,则
,则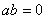 ”的否命题是:“若
”的否命题是:“若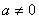 ,则
,则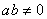 ”
”
C.命题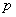 :
: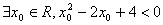 ,则
,则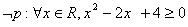
D.特称命题 “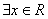 ,使
,使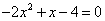 ”是真命题.
”是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
从黄瓜、白菜、油菜、扁豆4个蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,则不同的种植方法种数为 ( )
A.6种 B.12种 C.18种 D.24种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com