
分析 (Ⅰ)由正实数a,b,c满足a+b2+c3=1,运用三元均值不等式,可得ab2c3≤$\frac{1}{27}$,再由均值不等式即可得$\frac{1}{a^2}$+$\frac{1}{b^4}$+$\frac{1}{c^6}$的最小值m.
(Ⅱ)利用绝对值不等式的几何意义可求得|x-d|+|x+16|≥|x-d-x-16|=|d+16|,由题意及(Ⅰ)得,|d+16|≥27,从而可求得实数d的取值范围.
解答 解:(Ⅰ)因为正实数a,b,c满足a+b2+c3=1,
所以a+b2+c3=1≥$3\root{3}{a{b}^{2}{c}^{3}}$,即ab2c3≤$\frac{1}{27}$,当且仅当a=b2=c3时取等号,
所以$\frac{1}{a^2}$+$\frac{1}{b^4}$+$\frac{1}{c^6}$≥$3\root{3}{\frac{1}{{a}^{2}{b}^{4}{c}^{6}}}$≥27,
所以$\frac{1}{a^2}$+$\frac{1}{b^4}$+$\frac{1}{c^6}$的最小值m=27;
(Ⅱ)因为|x-d|+|x+16|≥|x-d-x-16|=|d+16|,
由题意及(Ⅰ)得,|d+16|≥27,得d≥11或d≤-43.
点评 本题考查不等式的证明,考查绝对值不等式的解法,掌握绝对值不等式的几何意义是解决问题的关键,注意运用三元均值不等式,考查化简整理的运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
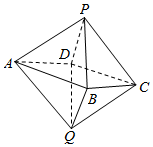 甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.
甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,AB=$\sqrt{2}$BC=2,∠BAD=45°,E为线段AB的动点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,则直线DC与平面A′DE所成角的最小值为( )
如图,在平行四边形ABCD中,AB=$\sqrt{2}$BC=2,∠BAD=45°,E为线段AB的动点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,则直线DC与平面A′DE所成角的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=$\frac{1}{2},φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2},φ=-\frac{π}{6}$ | C. | $ω=2,φ=\frac{π}{6}$ | D. | $ω=2,φ=-\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com