Question

19．已知AB为单位圆上的弦，P为单位圆上的点，若f（λ）=|$\overrightarrow{BP}$-λ$\overrightarrow{BA}$|的最小值为m（其中λ∈R），P在单位圆上运动时，m的最大值为$\frac{3}{2}$，则|$\overrightarrow{AB}$|的值为$\sqrt{3}$．

Answer 1

分析 设λ$\overrightarrow{BA}$=$\overrightarrow{BC}$，则$\overrightarrow{BP}$-λ$\overrightarrow{BA}$=$\overrightarrow{BP}$-$\overrightarrow{BC}$=$\overrightarrow{CP}$，而点C在直线AB上，则问题即是求动点P到直线AB上的点C距离的最值问题，则CP⊥AB时，距离最小，由CP过圆心O时，取得最大值，再由垂径定理和勾股定理，即可得到AB的长．

解答 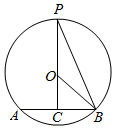解：设λ$\overrightarrow{BA}$=$\overrightarrow{BC}$，则$\overrightarrow{BP}$-λ$\overrightarrow{BA}$=$\overrightarrow{BP}$-$\overrightarrow{BC}$=$\overrightarrow{CP}$，
又C点在直线AB上，
要求f（λ）=|$\overrightarrow{BP}$-λ$\overrightarrow{BA}$|的最小值，
即求|$\overrightarrow{CP}$|的最小值，显然当CP⊥AB时，CP最小，
可得f（λ）的最小值m为点P到AB的距离
又m的最大值为$\frac{3}{2}$，可得CP过圆心O时m取得最大值，
即有|$\overrightarrow{AB}$|=2$\sqrt{{1}^{2}-（\frac{3}{2}-1）^{2}}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题考查向量共线定理的运用，以及圆的垂径定理和勾股定理的运用，同时考查最值的求法，注意运用几何方法和数形结合的思想方法，属于中档题．