
【题目】已知椭圆![]() 与直线y=
与直线y=![]() x-2
x-2![]() 相切,设椭圆的上顶点为M,
相切,设椭圆的上顶点为M, ![]() 是椭圆的左右焦点,且⊿M
是椭圆的左右焦点,且⊿M![]() 为等腰直角三角形。(1)求椭圆的标准方程;(2)直线l过点N(0,-
为等腰直角三角形。(1)求椭圆的标准方程;(2)直线l过点N(0,-![]() )交椭圆于A,B两点,直线MA、MB分别与椭圆的短轴为直径的圆交于S,T两点,求证:O、S、T三点共线。
)交椭圆于A,B两点,直线MA、MB分别与椭圆的短轴为直径的圆交于S,T两点,求证:O、S、T三点共线。
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

则参加测试的总人数为______,分数在![]() 之间的人数为______.
之间的人数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了全面贯彻党的教育方针,坚持以人文本、德育为先,全面推进素质教育,让学生接触自然,了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,减轻学生过重负担,培养学生兴趣爱好,丰富学生的课余生活,使广大学生在社会实践中,提高创新精神和实践能力,树立学生社会责任感,因此学校鼓励学生利用课余时间参加社会活动实践。寒假归来,某校高三(2)班班主任收集了所有学生参加社会活动信息,整理出如图所示的图。

(1)求高三(2)班同学人均参加社会活动的次数;
(2)求班上的小明同学仅参加1次社会活动的概率;
(3)用分层抽样的方法从班上参加活动2次及以上
的同学中抽取一个容量为5的样本,从这5人中任选3人,其中仅有两人参加2次活动的概率。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上运动.
上运动.
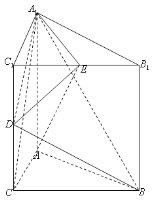
(1)求证![]()
![]()
![]() ;
;
(2)当点![]() 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)在(2)的条件下,试确定线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com