
分析 由已知⇒cotC=tan∠BAD⇒C+∠BAD=$\frac{π}{2}$⇒sin∠BAD=cosC,又因为∠BAD+C+∠CAD+B=π,故$∠CAD+B=\frac{π}{2}$⇒sin∠CAD=cosB,又$\frac{DB}{sin∠BAD}=\frac{AD}{sinB}$,$\frac{DC}{sin∠CAD}=\frac{AD}{sinC}$,得sinC•sin∠BAD=sinB•sin∠CAD⇒2B=2CB=C,即AB=AC.先在△ABE中利用余弦定理表示出cos∠BAC,进而求得sin∠BAC的表达式,进而代入三角形面积公式利用转化为二次函数来解决.
解答 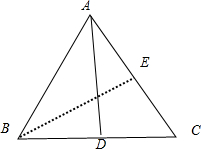 解:∵$\frac{\overrightarrow{CA}•\overrightarrow{CB}}{{S}_{△CAB}}$=4$\frac{{S}_{△ABD}}{\overrightarrow{AB}•\overrightarrow{AD}}$,∴$\frac{CA•CBcosC}{\frac{1}{2}CA•CBsinC}=4×\frac{\frac{1}{2}AB•ADsin∠BAD}{AB•ADcos∠BAD}$.
解:∵$\frac{\overrightarrow{CA}•\overrightarrow{CB}}{{S}_{△CAB}}$=4$\frac{{S}_{△ABD}}{\overrightarrow{AB}•\overrightarrow{AD}}$,∴$\frac{CA•CBcosC}{\frac{1}{2}CA•CBsinC}=4×\frac{\frac{1}{2}AB•ADsin∠BAD}{AB•ADcos∠BAD}$.
⇒cotC=tan∠BAD⇒C+∠BAD=$\frac{π}{2}$⇒sin∠BAD=cosC
又因为∠BAD+C+∠CAD+B=π,∴$∠CAD+B=\frac{π}{2}$⇒sin∠CAD=cosB
在△ABD中,$\frac{DB}{sin∠BAD}=\frac{AD}{sinB}$,…①
在△ADC中,$\frac{DC}{sin∠CAD}=\frac{AD}{sinC}$,…②
∵DB=DC,结合①②得sinC•sin∠BAD=sinB•sin∠CAD
∴sinB•cosB=sinC•cosC⇒sin2B=sin2C⇒2B=2C或2B+2C=π.
∵△ABC是非直角△,∴B=C,即AB=AC.
∵2$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\overrightarrow{BC}$,BE=2,则E为AC中点.
设AB=2x,则AE=x,在△ABE中,cos∠BAC=$\frac{{4x}^{2}+{x}^{2}-4}{2•2x•x}=\frac{5}{4}-\frac{1}{{x}^{2}}$
sin∠BAC=$\sqrt{1-(\frac{5}{4}-\frac{1}{{x}^{2}})^{2}}=\sqrt{-\frac{9}{16}-\frac{1}{{x}^{4}}+\frac{5}{2{x}^{2}}}$
$\frac{1}{2}×(2x)^{2}×\sqrt{-\frac{9}{16}-\frac{1}{{x}^{4}}+\frac{5}{2{x}^{2}}}$=$\frac{1}{2}\sqrt{-9({x}^{2}-\frac{20}{9})^{2}+\frac{256}{9}}$$≤\frac{8}{3}$
故当x=$\frac{2\sqrt{5}}{3}$时,△ABC的面积的最大值为$\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题主要考查了向量数量积的运算、余弦定理和正弦定理的运用.解题过程中充分利用好等腰三角形这个条件,把表达式的未知量减到最少.属于难题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 物理(x分) | 90 | 85 | 74 | 68 | 63 |
| 数学(y分) | 130 | 125 | 110 | 95 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
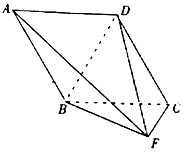 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com