Question

14．已知$\overrightarrow a=（sinx，cosx），\overrightarrow b=（sinx，sinx），f（x）=2\overrightarrow a•\overrightarrow b$．
（Ⅰ）求f（x）的最小正周期和最大值；
（Ⅱ）若$g（x）=f（x），x∈[{-\frac{π}{2}，\frac{π}{2}}]$，画出函数y=g（x）的图象，讨论y=g（x）-m（m∈R）的零点个数．

Answer 1

分析 （Ⅰ）根据f（x）=2$\overrightarrow{a}•\overrightarrow{b}$，利用向量数量积的运算法则求解f（x）并化简，即可求得f（x）的最小正周期和最大值
（Ⅱ）$g（x）=f（x），x∈[{-\frac{π}{2}，\frac{π}{2}}]$，利用“5点画法”画出函数y=g（x）的图象．

解答 解：（Ⅰ）f（x）=2$\overrightarrow{a}•\overrightarrow{b}$=2sinxcosx+2sin²x=sin2x-cos2x+1=$\sqrt{2}sin（{2x-\frac{π}{4}}）+1$
∴f（x）的最小正周期T=π；
函数f（x）的最大值为：$f{（x）_{max}}=\sqrt{2}+1$；
（Ⅱ）$g（x）=f（x），x∈[{-\frac{π}{2}，\frac{π}{2}}]$，利用“5点画法”，函数y=g（x）在区间$[{-\frac{π}{2}，\frac{π}{2}}]$上列表为

x	$-\frac{π}{2}$	$-\frac{3π}{8}$	$-\frac{π}{8}$	$\frac{π}{8}$	$\frac{3π}{8}$	$\frac{π}{2}$
$2x-\frac{π}{4}$	$-\frac{5π}{4}$	-π	$-\frac{π}{2}$	0	$\frac{π}{2}$	$\frac{3π}{4}$
$sin（{2x-\frac{π}{4}}）$	$\frac{{\sqrt{2}}}{2}$	0	-1	0	1	$\frac{{\sqrt{2}}}{2}$
$y=\sqrt{2}sin（{2x-\frac{π}{4}}）+1$	2	1	$1-\sqrt{2}$	1	$1+\sqrt{2}$	2

描点作图

那么：y=g（x）-m（m∈R）的零点个数，即为函数y=g（x）与直线y=m的交点个数，
由图可知，当$m＜1-\sqrt{2}或m＞1+\sqrt{2}$时，无零点；
当$m=1-\sqrt{2}或m=1+\sqrt{2}$时，有1个零点；
当$1-\sqrt{2}＜m＜2$或$2＜m＜1+\sqrt{2}$时，有2个零点；
当m=2时，有3个零点．

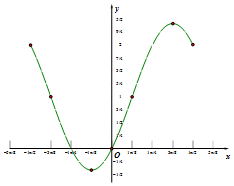
点评 本题主要考查三角函数的图象和性质，将零点问题转化为交点问题，利用“5点画法”作出图象是关键．