
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{4}$ | C. | $\sqrt{\frac{{1+\sqrt{5}}}{2}}$ | D. | $\frac{{\sqrt{3+\sqrt{5}}}}{2}$ |
分析 利用点F2到直线l的距离等于实半轴的长,可得$\frac{|2bc|}{\sqrt{{b}^{2}+{c}^{2}}}$=a,得出a与c之间的等量关系,进而求出离心率.
解答 解:由题意,直线l的方程为y=$\frac{b}{c}$x+b,即bx-cy+bc=0,
∵点F2到直线l的距离等于实半轴的长,
∴$\frac{|2bc|}{\sqrt{{b}^{2}+{c}^{2}}}$=a,
∴4(c2-a2)c2=a2(2c2-a2),
∴4e4-6e2+1=0,
∵e>1,∴e=$\frac{\sqrt{3+\sqrt{5}}}{2}$,
故选D.
点评 本题考查双曲线的方程与性质,考查点到直线距离公式的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | ±8 | D. | $±\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
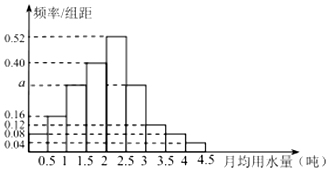 我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
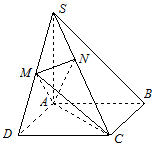 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1±$\sqrt{10}$ | B. | 1$±\sqrt{10}$ | C. | -1-$\sqrt{10}$ | D. | 1-$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com