
分析 (Ⅰ)由题意知|MF1|+|MF2|=2|F1F2|=8>4,所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.由此可知曲线C的方程;
(Ⅱ)设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.由$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\\{y=k(x+4)}\end{array}\right.$,得(3+4k2)y2-24ky=0,由此利用韦达定理、椭圆性质,结合已知条件能fiy bm 直线MN的方程.
解答 解:(Ⅰ)∵F1(-2,0),F2(2,0),∴|F1F2|=4,
∵|MF1|+|MF2|=8>4,
∴曲线C是以F1,F2为焦点,长轴长为8的椭圆.
曲线C的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1.(4分)
(Ⅱ)由题意知直线MN不垂直于x轴,也不与x轴重合或平行.(5分)
设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\\{y=k(x+4)}\end{array}\right.$,得(3+4k2)y2-24ky=0.
解得y=0或y=$\frac{24k}{4{k}^{2}+3}$.
依题意${y}_{M}=\frac{24k}{4{k}^{2}+3}$,xM=$\frac{1}{k}$yM-4=$\frac{-16{k}^{2}+12}{4{k}^{2}+3}$.(7分)
因为S△MNF2:S△PNF2=3:2,
所以$\frac{|M{F}_{2}|}{|{F}_{2}P|}$=$\frac{3}{2}$,则$\overrightarrow{M{F}_{2}}$=$\frac{3}{2}$$\overrightarrow{{F}_{2}P}$.
于是$\left\{\begin{array}{l}{2-{x}_{M}=\frac{3}{2}(0-{y}_{M})}\\{0-{y}_{M}=\frac{3}{2}({y}_{P}-0)}\end{array}\right.$,所以$\left\{\begin{array}{l}{{x}_{P}=\frac{2}{3}(2-{x}_{M})+2=\frac{24{k}^{2}+2}{4{k}^{2}+3}}\\{{y}_{P}=-\frac{2}{3}{y}_{M}=\frac{-16M}{4{k}^{2}+3}}\end{array}\right.$,(9分)
因为点P在椭圆上,所以3($\frac{24{k}^{2}+2}{4{k}^{2}+3}$)2+4($\frac{-16k}{4{k}^{2}+3}$)=48.
整理得48k4+8k2-21=0,
解得${k}^{2}=\frac{7}{12}$或k2=-$\frac{3}{4}$(舍去),
从而k=$±\frac{\sqrt{21}}{6}$.((11分))
所以直线MN的方程为y=$±\frac{\sqrt{21}}{6}$(x+4).(12分)
点评 本题考查椭圆的定义标准方程及其性质、直线方程的性质、斜率计算公式,考查了转化能力,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
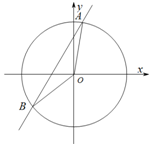 如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )
如图,在平面直角坐标系xoy中,直线y=2x+1与圆x2+y2=4相交于A,B两点,则cos∠AOB=( )| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $-\frac{{\sqrt{5}}}{10}$ | C. | $\frac{9}{10}$ | D. | $-\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
已知点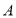 、
、 分别是椭圆
分别是椭圆 :
: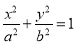 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: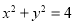 相切于点
相切于点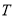 ,且点
,且点 是线段
是线段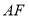 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆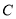 的标准方程为 .
的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
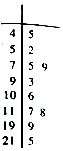
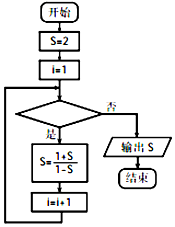 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )| A. | i≤2015? | B. | i≤2016? | C. | i≤2017? | D. | i≤2018? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com