练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设命题p：-6≤m≤6，命题函数q：f（x）=x2+mx+9（m∈R）没有零点，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 求出关于命题q的m的范围，根据集合的包含关系结合充分必要条件的定义判断即可．

    解答 解：∵f（x）=x2+mx+9（m∈R）没有零点，
    ∴△=m2-36＜0，解得：-6＜m＜6，
    ∴q：-6＜m＜6，而命题p：-6≤m≤6，
    故p是q的必要不充分条件，
    故选：B．

    点评 本题考查了充分必要条件，考查集合的包含关系，科学二次函数的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．函数f（x）=exlnx在点（1，f（1））处的切线方程是y=ex-e．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点F（-3，0），P为椭圆上一动点，椭圆内部点M（-1，3）满足PF+PM的最大值为17，则椭圆的离心率为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{2}}}{2}$C．$\frac{1}{3}$D．$\frac{{2\sqrt{3}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若曲线f（x）=$\frac{a}{2}$x2-ex不存在垂直于y轴的切线，则实数a的取值范围是[0，e）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

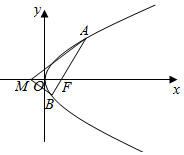    1．如图，AB是抛物线y2=2px（p＞0）的一条经过焦点F的弦，AB与两坐标轴不垂直，已知点M（-1，0），∠AMF=∠BMF，则p的值是（　　）
    A．$\frac{1}{2}$B．1C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．我校为了了解高三学生在大庆市第一次模拟考试中对数学的掌握情况，从高三年级中随机抽查了100名学生的数学成绩，并制成了频率直方图，从图中可以知道这100名学生的平均分数和中位数分别为（　　）
    A．103.2  113.2B．108.2  108C．103.2  108D．108.2  113.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知平面向量$\overrightarrow{a}$=（$\sqrt{3}$sinx，-1），$\overrightarrow{b}$=（2cosx，1-2cos2x），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
    （1）求函数f（x）的最小正周期，并写出f（x）的对称轴方程；
    （2）当x∈（-$\frac{5π}{6}$，-$\frac{π}{3}$）时，设经过函数f（x）图象上任意不同两点的直线的斜率为k，试判断k的符号，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知集合A={1，2，3}，B={m，3，6}，A∩B={2，3}，则实数m的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．一元二次不等式ax2+bx+c＜0的解集为R，则必有（　　）
    A．$\left\{\begin{array}{l}{a＞o}\\{{b}^{2}-4ac＞0}\end{array}\right.$B．$\left\{\begin{array}{l}{a＜0}\\{{b}^{2}-4ac＜0}\end{array}\right.$C．$\left\{\begin{array}{l}{a＞0}\\{{b}^{2}-4ac＜0}\end{array}\right.$D．$\left\{\begin{array}{l}{a＜0}\\{{b}^{2}-4ac＞0}\end{array}\right.$

    查看答案和解析>>

    同步练习册答案