
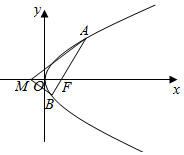
 如图,AB是抛物线y2=2px(p>0)的一条经过焦点F的弦,AB与两坐标轴不垂直,已知点M(-1,0),∠AMF=∠BMF,则p的值是( )
如图,AB是抛物线y2=2px(p>0)的一条经过焦点F的弦,AB与两坐标轴不垂直,已知点M(-1,0),∠AMF=∠BMF,则p的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 由题意画出图象作AC⊥x轴、BD⊥x轴,设AB的直线方程y=k(x-$\frac{p}{2}$)(k≠0),A(x1,y1)、B(x2,y2),联立直线方程和抛物线方程消去y,由韦达定理求出x1+x2和x1x2式子,由∠AMF=∠BMF得tan∠AMF=tan∠BMF,由图象得$\frac{AC}{MC}=\frac{BD}{MD}$,用A、B的坐标表示出线段的长,把求出的式子代入化简,列出关于p的方程再化简求值.
解答 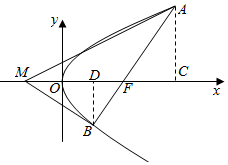 解:如右图作AC⊥x轴,BD⊥x轴,
解:如右图作AC⊥x轴,BD⊥x轴,
设AB的直线方程为:y=k(x-$\frac{p}{2}$)(k≠0),A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,得${k}^{2}{x}^{2}-({k}^{2}p+2p)x+\frac{{k}^{2}{p}^{2}}{4}=0$,
则x1+x2=$\frac{{k}^{2}p+2p}{{k}^{2}}$,x1x2=$\frac{{p}^{2}}{4}$,
∵∠AMF=∠BMF,∴tan∠AMF=tan∠BMF,
即$\frac{AC}{MC}=\frac{BD}{MD}$,
不妨设x1>$\frac{p}{2}$,x2<$\frac{p}{2}$,
则AC=|y1|=|k(x1-$\frac{p}{2}$)|=|k|(x1-$\frac{p}{2}$),BD=|y2|=|k(x2-$\frac{p}{2}$)|=|k|($\frac{p}{2}$-x2),
且MC=x1+1,MD=x2+1,
代入$\frac{AC}{MC}=\frac{BD}{MD}$得,$\frac{|k|({x}_{1}-\frac{p}{2})}{{x}_{1}+1}=\frac{|k|(\frac{p}{2}-{x}_{2})}{{x}_{2}+1}$,
化简得,2x1x2+(x1+x2)(1-$\frac{p}{2}$)-p=0,
则2×$\frac{{p}^{2}}{4}+\frac{{k}^{2}p+2p}{{k}^{2}}(1-\frac{p}{2})-p=0$,化简得$\frac{2-p}{{k}^{2}}=0$,得p=2.
故选:C.
点评 本题考查抛物线的简单性质,考查直线与抛物线的位置关系的应用,一元二次方程的根与系数的关系,考查化简计算能力,是中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,3) | B. | (-1,1)∪(1,3) | C. | [-1,1)∪(1,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{i+1}{2}$ | B. | $\frac{i-1}{2}$ | C. | $\frac{1-i}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$+2 | B. | $\sqrt{17}$+$\sqrt{5}$ | C. | $\sqrt{13}$+1 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com