
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,BC=$\sqrt{2}$,AD=DC=1.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,BC=$\sqrt{2}$,AD=DC=1.分析 (1)根据线面垂直的性质定理进行证明即可.
(2)根据条件求出四棱锥的高,利用棱锥的体积公式进行求解即可.
解答 证明:(1)∵PA⊥平面ABCD,BC?面ABCD,
∴PA⊥BC,连接AC,
∵AD=CD,AD⊥CD,∴AC=$\sqrt{2}$,
∵BC=$\sqrt{2}$,AB=2,AB2=AC2+BC2,
∴BC⊥AC,∴BC⊥面PAC,
∵PC?面PAC,
∴PC⊥BC;
(2)由(1)知BC⊥PC,且PC=$\sqrt{P{A}^{2}+A{C}^{2}}=\sqrt{6}$,
∵E为PB中点,F为BC中点,
∴SEFCP=$\frac{3}{4}$SPBC,
则VD-EFCP=$\frac{3}{4}$VD-PBC=$\frac{3}{4}$VP-DBC=$\frac{3}{4}×\frac{1}{3}•PA•({S}_{ABCD}-{S}_{ABD})$=$\frac{1}{4}×2×(\frac{3}{2}-1)=\frac{1}{4}$.
点评 本题主要考查空间直线和直线垂直的判定以及三棱锥体积的计算,根据相应的判定定理以及棱锥的体积公式是解决本题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
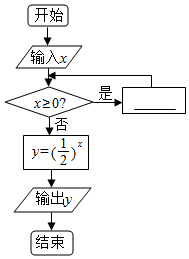 已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )
已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [1,3] | C. | [-1,11] | D. | [-5,11] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com