
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
[解析] (1)a=-2时,f(x)=x2-4x+3=(x-2)2-1,
∵x∈[-4,6],∴f(x)min=f(2)=-1,f(x)max=f(-4)=35.
(2)f(x)=x2+2ax+3=(x+a)2+3-a2,
要使f(x)在[-4,6]上是单调函数,
应有-a≤-4或-a≥6,∴a≥4或a≤-6.
(3)a=1时,f(x)=x2+2x+3=(x+1)2+2,f(|x|)=(|x|+1)2+2.
令t=|x|(-4≤x≤6),则0≤t≤6,
∵t=|x|在[-4,0]上单调递减,在[0,6]上单调递增,y=(t+1)2+2在[0,6]上单调递增,
∴f(|x|)在[-4,0]上单调递减,在[0,6]上单调递增.


科目:高中数学 来源: 题型:
已知定义域为R的函数f(x)=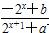 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=f(x)的定义域为R,并对一切实数x,都满足f(2+x)=f(2-x).
(1)证明:函数y=f(x)的图像关于直线x=2对称;
(2)若f(x)是偶函数,且x∈[0,2]时,f(x)=2x-1,求x∈[-4,0]时的f(x)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
若直角坐标平面内的两个不同点M,N满足条件:
①M,N都在函数y=f(x)的图象上;
②M,N关于原点对称.
则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为同一“友好点对”)
已知函数f(x)=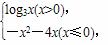 此函数的“友好点对”有( )
此函数的“友好点对”有( )
A.0对 B.1对
C.2对 D.3对
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2)、(0,1)内,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是( )
A.(-2,2) B.[-2,2]
C.(-∞,-1) D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司欲投资13亿元进行项目开发,现有以下6个项目可供选择.
| 项目 | A | B | C | D | E | F |
| 投资额(亿元) | 5 | 2 | 6 | 4 | 6 | 1 |
| 利润(亿元) | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 0.1 |
设计一个投资方案,使投资13亿元所获利润大于1.6亿元,则应选的项目是________(只需写出项目的代号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com