
已知定义域为R的函数f(x)=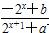 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
(1)∵f(x)是奇函数,
∴f(0)=0,即 =0,解得b=1,从而有f(x)=
=0,解得b=1,从而有f(x)= .
.
又由f(1)=-f(-1)知
解得a=2.经检验a=2适合题意,
∴所求a,b的值分别为2,1.
(2)解法1:由(1)知f(x)=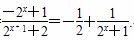
由上式易知f(x)在(-∞,+∞)上为减函数.
又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0,等价于
f(t2-2t)<-f(2t2-k)=f(-2t2+k).
因f(x)是减函数,由上式推得t2-2t>-2t2+k.
即对一切t∈R有3t2-2t-k>0.
从而判别式Δ=4+12k<0,解得k<-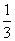 .
.
解法2:由(1)知f(x)=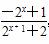 ,又由题设条件得
,又由题设条件得
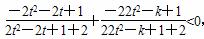 即(22t2-k+1+2)(-2t2-2t+1)+(2t2-2t+1+2)·(-22t2-k+1)<0.
即(22t2-k+1+2)(-2t2-2t+1)+(2t2-2t+1+2)·(-22t2-k+1)<0.
整理得23t2-2t-k>1,因底数2>1,故3t2-2t-k>0.
上式对一切t∈R均成立,从而判别式Δ=4+12k<0,解得k<-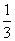 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
若函数y=4x-3·2x+3的定义域为集合A,值域为[1,7],集合B=(-∞,0]∪[1,2],则集合A与集合B的关系为( )
A.AB B.A=B
C.BA D.A⊆B
查看答案和解析>>
科目:高中数学 来源: 题型:
设a,b,c为均不等于1的正实数,则下列等式中恒成立的是( )
A.logab·logcb=logca
B.logab·logca=logcb
C.loga(bc)=logab·logac
D.loga(b+c)=logab+logac
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com