
| A. | 奇函数且它的图象关于点(π,0)对称 | |
| B. | 奇函数且它的图象关于点($\frac{3π}{4}$,0)对称 | |
| C. | 偶函数且它的图象关于直线x=π对称 | |
| D. | 偶函数且它的图象关于直线x=$\frac{3π}{4}$对称 |
分析 先对函数f(x)运用三角函数的辅角公式进行化简求出最小正周期,根据正弦函数的最值和取得最值时的x的值可求出函数y=|f($\frac{3π}{4}$-x)|的解析式,进而得到答案.
解答 解:已知函数f(x)=asinx-bcosx(a、b为常数,a≠0,x∈R),
∴f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(x-φ)的周期为2π,若函数在x=$\frac{π}{4}$处取得最小值,不妨设f(x)=sin(x-$\frac{3π}{4}$),
则函数y=f( $\frac{3π}{4}$-x)=sin( $\frac{3π}{4}$-x-$\frac{3π}{4}$)=-sinx,
所以函数y=|f($\frac{3π}{4}$-x)|=|-sinx|=|sinx|是偶函数且它的图象关于直线x=π对称,
故选:C.
点评 本题主要考查辅角公式、三角函数的奇偶性和对称性.对于三角函数的基本性质要熟练掌握,这是解题的根本.


科目:高中数学 来源: 题型:解答题
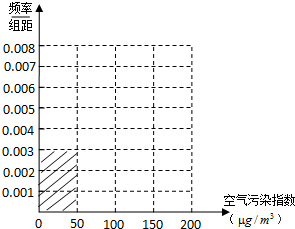
| 空气污染指数 (单位:μg/m3) | (0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
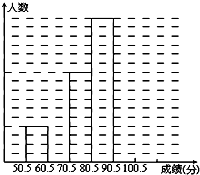 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | a | 0.16 |
| 70.5~80.5 | 10 | b |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | c | d |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com