每日10分钟口算心算速算天天练系列答案科目：高中数学 来源： 题型：
已知f(x)＝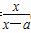
(x≠a)．
(1)若a＝－2，试证f(x)在(－∞，－2)内单调递增；
(2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
经市场调查，某商品在过去100天内的销售量和价格均为时间t(天)的函数，且日销售量近似地满足g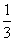(t)＝－
t＋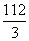
(1≤t≤100，t∈N)．前40天价格为f(t)＝
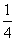t＋22(1≤t≤40，t∈N)，后60天价格为f(t)＝－
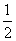t＋52(41≤t≤100，t∈N)，试求该商品的日销售额S(t)的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
设函数f(x)＝ax2＋bx＋c(a、b、c为实数，且a≠0)，F(x)＝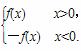
(1)若f(－1)＝0，曲线y＝f(x)通过点(0,2a＋3)，且在点(－1，f(－1))处的切线垂直于y轴，求F(x)的表达式；
(2)在(1)的条件下，当x∈[－1,1]时，g(x)＝kx－f(x)是单调函数，求实数k的取值范围；
(3)设mn<0，m＋n>0，a>0，且f(x)为偶函数，证明F(m)＋F(n)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
) B．(
) D．(
－
的定义域为________．
，则f(－1)＝( )
，且当x∈[－3，－1]时，n≤f(x)≤m恒成立，则m－n的最小值是________．
，2)在幂函数y＝f(x)的图像上，点(－
)在幂函数y＝g(x)的图像上，若f(x)＝g(x)，则x＝______.