
分析 (1)求导,由题意可得f'(1)=1,代入即可求得a,b的值;
(2)分别利用导数求出函数f(x),g(x)的最值,再比较判断,即可证明.
解答 解:(1)当x=1时,y=e,即f(1)=ae=e,解得a=1,
∵f′(x)=ex(x2+2x)+$\frac{b}{x}$,
∴f′(1)=e(1+2)+b=3e-1,解得b=-1,
(2)证明:由(1)得f′(x)=ex(x2+2x)-$\frac{1}{x}$,
令h(x)=ex(x2+2x)-$\frac{1}{x}$,
∴h′(x)=ex(x2+4x+2)+$\frac{1}{{x}^{2}}$,
∴h(x)为增函数,
∵f($\frac{1}{4}$)=$\frac{9}{16}{e}^{\frac{1}{4}}$-4<${e}^{\frac{1}{4}}$-4<2-4<0,f(1)=3e-1>0,
∴存在唯一的x1∈($\frac{1}{4}$,1),使得f′(x)=0,
即${e}^{{x}_{1}}$(x12+2x1)-$\frac{1}{{x}_{1}}$=0,
亦即2lnx1+ln(x1+2)+x1=0,
且f(x)在(0,x1)为减函数,在(x1,+∞)为增函数,
∴f(x)min=f(x1)=${e}^{{x}_{1}}$x12+lnx1=$\frac{{x}_{1}^{2}}{({x}_{1}^{2}+2{x}_{1}){x}_{1}}$-lnx1=$\frac{1}{{x}_{1}+2}$-lnx1,
∵g′(x)=-$\frac{2}{{x}^{2}}$ln(x-2)+($\frac{2}{x}$-1)$\frac{1}{x-2}$+$\frac{2-lnx}{{x}^{2}}$=$\frac{-2ln(x-2)-x+2-lnx}{{x}^{2}}$,
令φ(x)=-2ln(x-2)-x+2-lnx,则φ(x)在(2,+∞)上为减函数,
∵φ(3)=-3+2-ln3=-1-ln3<0,φ(2+$\frac{1}{{e}^{2}}$)=4-(2+$\frac{1}{{e}^{2}}$)+2-ln(2+$\frac{1}{{e}^{2}}$)>4-(2+1)+2-1>0,
∴存在唯一的x2∈(2+$\frac{1}{{e}^{2}}$,3),使得φ(x2)=0,
即φ(x2)=-2ln(x2-2)-x2+2-lnx2=0
亦即lnx2+2ln(x2+2)+x2-2=0,
且g(x)在(2,x2)为增函数,在(x2,+∞)为减函数,
∴g(x)max=g(x2)=($\frac{2}{{x}_{2}}$-1)ln(x2-2)+$\frac{ln{x}_{2}-1}{{x}_{2}}$+1
=($\frac{2}{{x}_{2}}$-1)ln(x2-2)+$\frac{-2ln({x}_{2}-2)-{x}_{2}+2-1}{{x}^{2}}$+1,
=$\frac{1}{{x}_{2}}$[(2-x2)ln(x2-2)-2ln(x2-2)-x2+1]+1
=$\frac{1}{{x}_{2}}$[-x2ln(x2-2)-x2+1]+1
=$\frac{1}{{x}_{2}}$-ln(x2-2),
∵2lnx1+ln(x1+2)+x1=2ln[(x1+2)-2]+ln(x1+2)+(x1+2)-2=0
∴x1+2=x2,
∴g(x)max=$\frac{1}{{x}_{2}}$-ln(x2-2)=$\frac{1}{{x}_{1}+2}$-lnx1=f(x)min;
问题得以证明.
点评 本题考查导数的综合应用,导数的几何意义,考查导数与函数的单调性和最值的关系,考查计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | Sn=2Tn | B. | Tn=2bn+1 | C. | Tn>an | D. | Tn<bn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
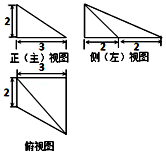
| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com