
分析 由条件利用三角函数在各个象限中的符号、同角三角函数的基本关系,求得m的值,可得tanθ的值.
解答 解:∵sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$,且θ为第四象限角,∴sinθ=$\frac{m-3}{m+5}$<0,cosθ=$\frac{4-2m}{m+5}$>0,
求得-5<m<2.
再根据sin2θ+cos2θ=${(\frac{m-3}{m+5})}^{2}$+${(\frac{4-2m}{m+5})}^{2}$=1,可得m=0,或m=8(舍去),
则tanθ=$\frac{sinθ}{cosθ}$=$\frac{m-3}{4-2m}$=-$\frac{3}{4}$,
故答案为:-$\frac{3}{4}$.
点评 本题主要考查同角三角函数的基本关系,三角函数在各个象限中的符号,属于基础题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
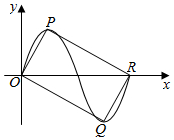 如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$]∪[$\frac{1}{2015}$,$\frac{1}{2014}$) | B. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$)∪($\frac{1}{2015}$,$\frac{1}{2014}$) | ||
| C. | (-$\frac{1}{2013}$,-$\frac{1}{2014}$]∪[$\frac{1}{2016}$,$\frac{1}{2015}$) | D. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$]∪[$\frac{1}{2016}$,$\frac{1}{2015}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com