
(12分)已知数列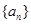 的前
的前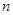 项和为
项和为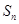 ,且
,且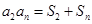 对一切正整数
对一切正整数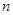 都成立.
都成立.
(1)求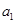 ,
,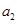 的值;
的值;
(2)设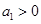 ,数列
,数列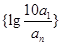 的前
的前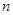 项和为
项和为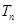 ,当
,当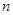 为何值时,
为何值时,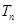 最大?并求出
最大?并求出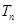 的最大值.
的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知各项都不相等的等差数列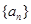 的前6项和为60,且
的前6项和为60,且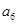 为
为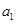 和
和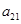 的等比中项.
的等比中项.
( I ) 求数列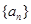 的通项公式;
的通项公式;
(II) 若数列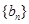 满足
满足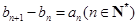 ,且
,且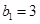 ,求数列
,求数列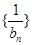 的前
的前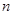 项和
项和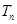 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知{an}为等差数列,且a3=-6,a6=0.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},
求{bn}的前n项和
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在从2011年到2014年期间,甲每年1月1日都到银行存入 元的一年定期储蓄。若年利率为
元的一年定期储蓄。若年利率为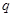 保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
A.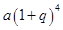 | B.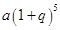 |
C.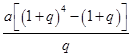 | D.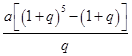 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com