Question

6．已知△ABC中，AB=2，AC=1，当2x+y=t（t＞0）时，|x$\overrightarrow{AB}$+y$\overrightarrow{AC}$|≥$\frac{\sqrt{2}}{2}$t恒成立，则△ABC的面积为1，在前述条件下，对于△ABC内一点P，$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值是-$\frac{5}{8}$．

Answer 1

分析 不等式|x$\overrightarrow{AB}$+y$\overrightarrow{AC}$|≥$\frac{\sqrt{2}}{2}$t，两边平方，结合向量的数量积的性质和二次不等式恒成立思想，解不等式可得cosA的范围，进而得到所求面积的值；由向量共线和数量积的定义，结合直角三角形的中线性质，以及基本不等式的运用，即可得到最小值．

解答 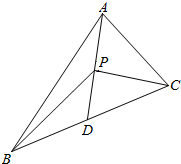解：不等式|x$\overrightarrow{AB}$+y$\overrightarrow{AC}$|≥$\frac{\sqrt{2}}{2}$t，
两边平方可得，x²$\overrightarrow{AB}$²+y²$\overrightarrow{AC}$²+2xy$\overrightarrow{AB}$•$\overrightarrow{AC}$≥$\frac{1}{2}$t²，
由AB=2，AC=1，2x+y=t，可得
4x²+y²+4xy（2cosA-1）≥0，
由判别式16y²（2cosA-1）²-16y²≤0，
即为cosA（cosA-1）≤0，
可得cosA≥0，即A的最大值为$\frac{π}{2}$，
当cosA=0时，|x$\overrightarrow{AB}$+y$\overrightarrow{AC}$|=$\sqrt{4{x}^{2}+{y}^{2}}$≥$\frac{\sqrt{2}}{2}$（2x+y），
则△ABC的面积为S=$\frac{1}{2}$AB•AC•sinA=$\frac{1}{2}×2×1$=1；
在直角三角形ABC中，取BC的中点D，连接PD，
则$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{PD}$，
则$\overrightarrow{PA}•（\overrightarrow{PB}+\overrightarrow{PC}）$=2$\overrightarrow{PA}$•$\overrightarrow{PD}$，
当A，P，D三点共线时，$\overrightarrow{PA}$•$\overrightarrow{PD}$＜0，
又此时AD=$\frac{1}{2}$BC=$\frac{\sqrt{5}}{2}$，
即有2$\overrightarrow{PA}$•$\overrightarrow{PD}$=-2|$\overrightarrow{PA}$|•|$\overrightarrow{PD}$|
≥-2•（$\frac{|\overrightarrow{PA}|+|\overrightarrow{PD}|}{2}$）²=-2•$\frac{5}{16}$=-$\frac{5}{8}$．
故答案为：1，-$\frac{5}{8}$．

点评 本题考查向量的数量积的定义和性质，考查不等式恒成立思想的运用，以及基本不等式的运用，考查运算能力，属于中档题．