已知函数f(x)=a2x+ax-6,其中a>0且a≠1.
(1)当a=2时,求函数f(x)的零点;
(2)若x∈[1,2]时,函数f(x)的最大值为6,求a的值.
解:(1)当a=2时,f(x)=2
2x+2
x-6…1分
由f(x)=0得2
2x+2
x-6=0,即(2
x-2)(2
x+3)=0…2分
∴2
x=2或2
x=-3(舍去) …4分
∴x=1…5分
∴函数f(x)的零点是1…6分
(2)令a
x=t,则g(t)=t
2+t-6
①当0<a<1时
∵函数t=a
x在R上是减函数,且1≤x≤2,∴a
2≤t≤a…7分
∵g(t)=t
2+t-6在
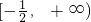
上单调递增
∴f(x)
max=g(t)
max=g(a)=6
∴a
2+a-6=6,即a
2+a-12=0…8分
解得a=3(舍去)或a=-4(舍去) …9分
②当a>1时
∵函数t=a
x在R上是增函数,且1≤x≤2,∴a≤t≤a
2…10分
∵g(t)=t
2+t-6在
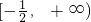
上单调递增
∴

∴(a
2)
2+a
2-6=6,即(a
2)
2+a
2-12=0…11分
解得a
2=3或a
2=-4(舍去) …12分
∴

…13分
综合①②可知,

. …14分.
分析:(1)求出f(x)=0的根,即可求函数f(x)的零点;
(2)换元,再进行分类讨论,利用函数的单调性,函数f(x)的最大值为6,即可求a的值.
点评:本题考查函数的零点,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

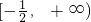 上单调递增
上单调递增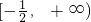 上单调递增
上单调递增
 …13分
…13分 . …14分.
. …14分.
