
如图,四棱锥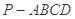 中,底面
中,底面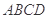 为正方形,
为正方形,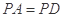
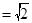 ,
,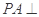 平面
平面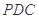 ,
,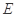 为棱
为棱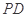 的中点.
的中点.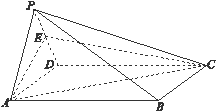
(1)求证:平面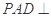 平面
平面 ;
;
(2)求二面角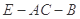 的余弦值.
的余弦值.
(3)求点 到平面
到平面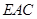 的距离.
的距离.
(1)要证明面面垂直,根据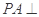 平面
平面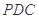 ,所以
,所以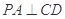 以及
以及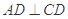 得到
得到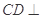 平面
平面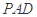 .从而得到证明。
.从而得到证明。
(2)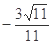 (3)
(3)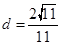
解析试题分析:(1)证明:因为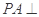 平面
平面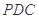 ,所以
,所以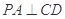 . 2分
. 2分
因为四边形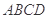 为正方形,所以
为正方形,所以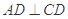 ,
,
所以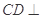 平面
平面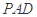 .
.
所以平面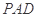
 平面
平面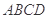 . 4分
. 4分
(2)解:在平面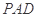 内过
内过 作直线
作直线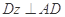 .
.
因为平面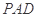
 平面
平面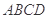 ,所以
,所以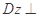 平面
平面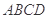 .
.
由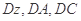 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系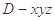 .
.
设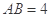 ,则
,则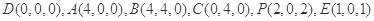 .
.
所以 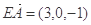 ,
,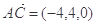 .
.
设平面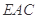 的法向量为
的法向量为 ,则有
,则有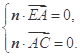
所以 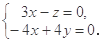 取
取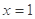 ,得
,得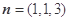 .
.
易知平面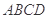 的法向量为
的法向量为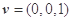 .
.
所以 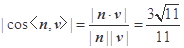 .
.
由图可知二面角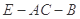 的平面角是钝角,
的平面角是钝角,
所以二面角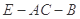 的余弦值为
的余弦值为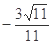 . 8分
. 8分
(3)根据等体积法可知 到平面
到平面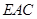 的距离,则可以利用
的距离,则可以利用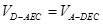 ,那么结合底面积和高可知
,那么结合底面积和高可知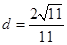 12分
12分
考点:二面角和距离
点评:主要是考查了空间中的面面垂直的判定定理和二面角以及点到面的距离的求解,属于中档题。


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
如图: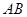 是⊙
是⊙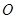 的直径,
的直径,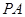 垂直于⊙
垂直于⊙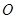 所在的平面,PA="AC,"
所在的平面,PA="AC," 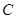 是圆周上不同于
是圆周上不同于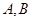 的任意一点,(1) 求证:
的任意一点,(1) 求证: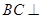 平面
平面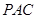 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。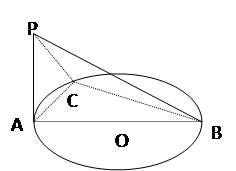
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,空间四边形 的对棱
的对棱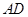 、
、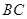 成
成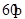 的角,且
的角,且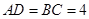 ,平行于
,平行于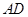 与
与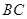 的截面分别交
的截面分别交 、
、 、
、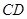 、
、 于
于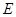 、
、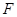 、
、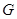 、
、 .
.
(1)求证:四边形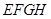 为平行四边形;
为平行四边形;
(2)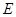 在
在 的何处时截面
的何处时截面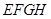 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com