
分析 先根据三角函数的性质,得到f(x)≥x2+$\frac{4}{{x}^{2}}$-$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}}$-(x+$\frac{2}{x}$),令t=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}}$≥$\sqrt{4}$=2,构造函数g(t)=t2-t-$\sqrt{{t}^{2}+4}$,t≥2,根据函数的单调性质求出g(t)的最小值,问题得以解决.
解答 解:f(x)=x2+$\frac{4}{{x}^{2}}$-x(cosθ+1)-$\frac{2}{x}$(sinθ+1)≥=x2+$\frac{4}{{x}^{2}}$-xcosθ-$\frac{2}{x}$sinθ-x-$\frac{2}{x}$=x2+$\frac{4}{{x}^{2}}$-$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}}$cos(θ+φ)-(x+$\frac{2}{x}$)≥x2+$\frac{4}{{x}^{2}}$-$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}}$-(x+$\frac{2}{x}$),
∵f(x)≥M恒成立,
即f(x)min≥M,
令t=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}}$≥$\sqrt{4}$=2,
∴g(t)=t2-t-$\sqrt{{t}^{2}+4}$,t≥2,
∴g′(t)=2t-1-$\frac{t}{\sqrt{{t}^{2}+4}}$=(2-$\frac{1}{\sqrt{{t}^{2}+4}}$)t-1
∴g′(2)=(2-$\frac{1}{2\sqrt{2}}$)×2-1=3-$\frac{\sqrt{2}}{2}$>0,
∴g(t)在[2,+∞)上单调递增,
即g(t)min=22-2-2$\sqrt{2}$=2-2$\sqrt{2}$,
∴f(x)min=2-2$\sqrt{2}$,当t=2时,x=$\sqrt{2}$时,cos(θ+φ)=1时取等号,
∴实数M的取值范围是(-∞,2-2$\sqrt{2}$],
故答案为:(-∞,2-2$\sqrt{2}$].
点评 本题考查了函数恒成立的问题,关键是构造函数,利用函数的单调性质求出函数的最值,培养克学生的转化能力,运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
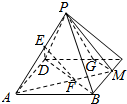 如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM.
如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{5}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com