
分析 一方面利用an>0可知$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$≥$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$=$\frac{6}{5}$,另一方面利用当n≥3时3n-2n>5•2n-2及等比数列的求和公式计算即得结论.
解答 证明:∵an=3n-2n,
∴当n≥3时,3n-2n>5•2n-2,
∵an>0,
∴$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$≥$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$=$\frac{1}{3-2}$+$\frac{1}{{3}^{2}-{2}^{2}}$=$\frac{6}{5}$,
$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$≤$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+$\frac{1}{5}$($\frac{1}{2}$+…+$\frac{1}{{2}^{n-2}}$)
=$\frac{6}{5}$+$\frac{1}{5}$•$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n-2}})}{1-\frac{1}{2}}$
=$\frac{6}{5}$+$\frac{1}{5}$•(1+$\frac{1}{{2}^{n-2}}$)
<$\frac{6}{5}$+$\frac{1}{5}$
=$\frac{7}{5}$,
综上所述,$\frac{6}{5}$≤$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$\frac{7}{5}$(n≥2).
点评 本题考查不等式的证明,利用放缩法是解决本题的关键,注意解题方法的积累,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
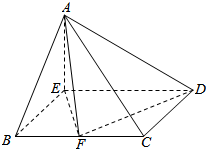 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com