
分析 (1)利用$S=\frac{1}{2}acsinB$即可得出.
(2)S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×\frac{{a}^{2}sinBsinC}{sinA}$,即可得出;
(3)p=$\frac{1}{2}(a+b+c)$,利用海伦公式可得S=$\sqrt{p(p-a)(p-b)(p-c)}$.
解答 解:(1)$S=\frac{1}{2}acsinB$=$\frac{1}{2}×28×33×\frac{\sqrt{2}}{2}$≈326.63.
(2)由正弦定理可得:$b=\frac{asinB}{sinA}$,$c=\frac{asinC}{sinA}$,
∴S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×\frac{asinB}{sinA}×\frac{asinC}{sinA}×sinA$=$\frac{1}{2}×\frac{{a}^{2}sinBsinC}{sinA}$=$\frac{1}{2}×\frac{3{6}^{2}×sin80.{7}^{°}×sin66.{5}^{°}}{sin32.{8}^{°}}$=$\frac{1}{2}×\frac{1296×0.9869×0.9170}{0.5417}$=1082.58.
(3)p=$\frac{1}{2}(a+b+c)$=93.
∴S=$\sqrt{p(p-a)(p-b)(p-c)}$=$\sqrt{93×39×32×22}$=24$\sqrt{4433}$≈24×66.58≈1597.92.
点评 本题考查了三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
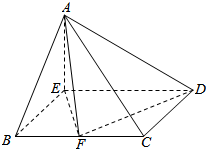 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com