
分析 对四个命题分别进行判断,即可得出结论.
解答 解:①命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0”,故不正确;
②f(x+$\frac{π}{2}$)=|sin(x+$\frac{π}{2}$)|+|cos(x+$\frac{π}{2}$)|=|cosx|+|sinx|,则f(x)的最小正周期是$\frac{π}{2}$,故不正确;
③若将一组样本数据中的每个数据都加上同一个常数后,则平均数加上常数,样本的方差不变,故正确;
④α∥β,a?α,b?β,与两个平面垂直的直线,与直线a,b垂直,故必存在与a,b都垂直的直线,所以正确.
故答案为:③④.
点评 本题考查命题真假的判断,考查命题的否定、f(x)的最小正周期,考查样本的方差,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
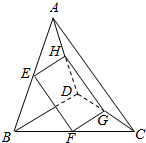 如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,三棱锥A-BCD中,AB=BC=CD=DA=BD=AC=2a,E,F,G,H分别是AB,BC,CD,DA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
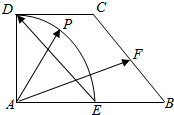 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com