
分析 (Ⅰ)求出两个函数的导函数,利用函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线,列出方程,即可求出b.
(Ⅱ)求出导函数f'(x),通过-1≤a≤1时,判断函数的单调性,当a2>1时,判断导函数的符号,判断函数的单调性.
(Ⅲ)令h(x)=g'(x)-f'(x)=ex-x2-2ax-1,求出导函数h'(x)=ex-2x-2a,令u(x)=h'(x)=ex-2x-2a,求出u'(x)=ex-2.通过当$a≤\frac{1}{2}$时,利用函数的单调性与最值求解即可.
解答 解:(Ⅰ)f'(x)=x2+2ax+b,g'(x)=ex,
由f'(0)=b=g'(0)=1,得b=1.…(2分)
(Ⅱ)f'(x)=x2+2ax+1=(x+a)2+1-a2,
当a2≤1时,即-1≤a≤1时,f'(x)≥0,从而函数f(x)在定义域内单调递增,
当a2>1时,$f'(x)=({x+a+\sqrt{{a^2}-1}})({x+a-\sqrt{{a^2}-1}})$,此时
若$x∈({-∞,-a-\sqrt{{a^2}-1}})$,f'(x)>0,则函数f(x)单调递增;
若$x∈({-a-\sqrt{{a^2}-1},-a+\sqrt{{a^2}-1}})$,f'(x)<0,则函数f(x)单调递减;
若$x∈({-a+\sqrt{{a^2}-1},+∞})$时,f'(x)>0,则函数f(x)单调递增.…(6分)
(Ⅲ)令h(x)=g'(x)-f'(x)=ex-x2-2ax-1,
则h(0)=e0-1=0.h'(x)=ex-2x-2a,令u(x)=h'(x)=ex-2x-2a,则u'(x)=ex-2.
当$a≤\frac{1}{2}$时,u(0)=h'(0)=1-2a≥0,
又当x≤0时,u'(x)<0,从而u(x)单调递减;
所以u(x)>0.
故当x∈(-∞,0)时,h(x)单调递增;
又因为h(0)=0,故当x<0时,h(x)<0,
从而函数g(x)-f(x)在区间(-∞,0)单调递减;
又因为g(0)-f(0)=0
所以g(x)>f(x)在区间(-∞,0)恒成立.…(14分)
点评 本题主要考查导数的运算、导数在研究函数中的应用、函数的零点等基础知识,考查推理论证能力、运算求解能力、创新意识,考查函数与方程、数形结合、分类与整合、化归与转化等数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
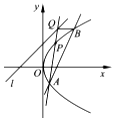 已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.
已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}-\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{3}{4}+\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{42}$ | B. | $\frac{1}{2}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com