
分析 (1)由于$|{P{F_1}}|•|{P{F_2}}|≤{({\frac{{|{P{F_1}}|+|{P{F_2}}|}}{2}})^2}={a^2}$,则|PF1|•|PF2|的最大值为a2,a2=25,a-c=1,c=4,即可求得b的值,求得椭圆T的方程;
(2)设直线AB的方程为y=kx+m,代入椭圆方程,由直线与圆相切代入即可求得A,B坐标,由两点之间的距离公式,利用韦达定理即可求得A、B两点间的距离|AB|的最大值;
(3)设G、H、D的坐标分别为(x1,y1),(x2,y2),(x,y),由题设知$|{\overrightarrow{GC}}|,|{\overrightarrow{HD}}|,|{\overrightarrow{GD}}|,|{\overrightarrow{CH}}|$,于是$\left\{\begin{array}{l}10=\frac{{{x_1}-λ{x_2}}}{1-λ}\\ 1=\frac{{{y_1}-λ{y_2}}}{1-λ}\end{array}\right.$且$\left\{\begin{array}{l}x=\frac{{{x_1}+λ{x_2}}}{1+λ}\\ y=\frac{{{y_1}+λ{y_2}}}{1+λ}\end{array}\right.$.从而$\left\{\begin{array}{l}10x=\frac{{{x_1}^2-{λ^2}{x_2}^2}}{{1-{λ^2}}}\\ y=\frac{{{y_1}^2-{λ^2}{y_2}^2}}{{1-{λ^2}}}\end{array}\right.$.又G、H在椭圆上,则$\left\{\begin{array}{l}9{x_1}^2+25{y_1}^2=9×25\\ 9{x_2}^2+25{y_2}^2=9×25\end{array}\right.$,化简整理得点D在定直线18x+5y-45=0上.
解答 解:(1)由于$|{P{F_1}}|•|{P{F_2}}|≤{({\frac{{|{P{F_1}}|+|{P{F_2}}|}}{2}})^2}={a^2}$,
所以|PF1|•|PF2|的最大值为a2,
当|PF1|=|PF2|时取等号,由已知可得a2=25,即a=5,又a-c=1,c=4,
所以b2=a2-c2=9,
故椭圆的方程为$\frac{x^2}{25}+\frac{y^2}{9}=1$.
(2)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,设直线AB的方程为y=kx+m.
因为A既在椭圆上,又在直线AB上,从而有$\left\{\begin{array}{l}\frac{x^2}{25}+\frac{y^2}{9}=1\\ y=kx+m\end{array}\right.$,消y得(25k2+9)x2+50kmx+25(m2-9)=0.
由于直线与椭圆相切,故,△=(50km)2-4(25k2+9)×25(m2-9)=0,
从而可得m2=9+25k2①,且${x_1}=\frac{-25k}{m}$②.
由$\left\{\begin{array}{l}{x^2}+{y^2}={R^2}\\ y=kx+m\end{array}\right.$,消y得(k2+1)x2+2kmx+m2-R2=0.由于直线与椭圆相切,得m2=R2(1+k2)③,且${x_2}=-\frac{{k{R^2}}}{m}$④.
由①③得${k^2}=\frac{{{R^2}-9}}{{25-{R^2}}}$,
故${|{AB}|^2}={({{x_2}-{x_1}})^2}+{({{y_2}-{y_1}})^2}=({1+{k^2}}){({{x_2}-{x_1}})^2}$,
=$\frac{m^2}{R^2}•\frac{{{k^2}{{({25-{R^2}})}^2}}}{m^2}=\frac{{{R^2}-9}}{R^2}•\frac{{{{({25-{R^2}})}^2}}}{{25-{R^2}}}=25+9-{R^2}-\frac{225}{R^2}$,
$≤34-2\sqrt{{R^2}×\frac{225}{R^2}}=34-30=4$,即|AB|≤2.
当且仅当$R=\sqrt{15}$时取等号,所以|AB|的最大值为2.
(3)证明:设G、H、D的坐标分别为(x1,y1),(x2,y2),(x,y),由题设知$|{\overrightarrow{GC}}|,|{\overrightarrow{HD}}|,|{\overrightarrow{GD}}|,|{\overrightarrow{CH}}|$,
均不为零,记$\frac{{|{\overrightarrow{GC}}|}}{{|{\overrightarrow{CH}}|}}=\frac{{|{\overrightarrow{GD}}|}}{{|{\overrightarrow{DH}}|}}=λ$,则λ>0且λ≠1,又C、G、D、H四点共线,则$\overrightarrow{GC}=-λ\overrightarrow{CH},\overrightarrow{GD}=λ\overrightarrow{DH}$.
于是$\left\{\begin{array}{l}10=\frac{{{x_1}-λ{x_2}}}{1-λ}\\ 1=\frac{{{y_1}-λ{y_2}}}{1-λ}\end{array}\right.$且$\left\{\begin{array}{l}x=\frac{{{x_1}+λ{x_2}}}{1+λ}\\ y=\frac{{{y_1}+λ{y_2}}}{1+λ}\end{array}\right.$.从而$\left\{\begin{array}{l}10x=\frac{{{x_1}^2-{λ^2}{x_2}^2}}{{1-{λ^2}}}\\ y=\frac{{{y_1}^2-{λ^2}{y_2}^2}}{{1-{λ^2}}}\end{array}\right.$.
又G、H在椭圆上,则$\left\{\begin{array}{l}9{x_1}^2+25{y_1}^2=9×25\\ 9{x_2}^2+25{y_2}^2=9×25\end{array}\right.$,消去x1,y1,x2,y2得90x+25y=9×25,
即点D在定直线18x+5y-45=0上.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,直线与圆的位置关系,考查基本不等式的应用,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
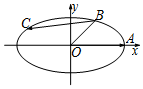 如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].
如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 零件个数x(个) | 1 | 2 | 3 | 4 |
| 加工时间y(小时) | 2 | 3 | 5 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8,4,3 | B. | 6,5,4 | C. | 7,5,3 | D. | 8,5,2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com