
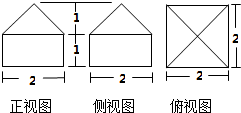
 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.分析 由已知中的三视图,可知该几何体是一个长方体和四棱锥的组合体,
(Ⅰ)分别计算长方体和四棱锥的体积,相加可得该几何体的体积;
(Ⅱ)分别计算各个面的面积,相加可得求该几何体的表面积.
解答 解:由图知该几何体上面是四棱锥下面是长方体,
长方体的长,宽,高,分别为2,2,1,棱锥的底面是边长为2的正方形,高为1,
(Ⅰ)体积V=2×2×1+$\frac{1}{3}$×2×2×1=$\frac{16}{3}$…(4分)
(Ⅱ)棱锥的侧高为$\sqrt{{1}^{2}+(\frac{2}{2})^{2}}$=$\sqrt{2}$
故表面积S=2×2+4×2×1+4×$\frac{1}{2}$×2×$\sqrt{2}$=12+4$\sqrt{2}$…(8分)
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
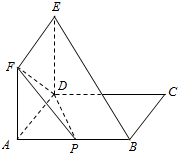 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
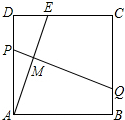 在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )| A. | 5:12 | B. | 5:13 | C. | 5:19 | D. | 5:21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$] | B. | [$\sqrt{3}$,2) | C. | (1,2) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com