Question

9．已知函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=（x+1）e^x则对任意的m∈R，函数F（x）=f（f（x））-m的零点个数至多有（　　）

• A． 3个
• B． 4个
• C． 6个
• D． 9个

Answer 1

分析 当x＜0时，f（x）=（x+1）e^x，求出f′（x），判断x∈（-∞，-2），函数是减函数，x∈（-2，0）函数是增函数，f（-2）=$-\frac{1}{{e}^{2}}$，f（-1）=0，且x→0时，f（x）→1，利用函数是奇函数，f（0）=0，画出函数的图象利用换元法，转化求解函数的零点个数即可．

解答 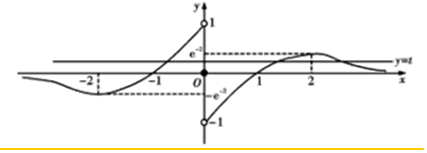解：当x＜0时，f（x）=（x+1）e^x，可得f′（x）=（x+2）e^x，可知x∈（-∞，-2），函数是减函数，x∈（-2，0）函数是增函数，
f（-2）=$-\frac{1}{{e}^{2}}$，f（-1）=0，且x→0时，f（x）→1，又f（x）是定义在R上的奇函数，f（0）=0，而x∈（-∞，-1）时，f（x）＜0，
所以函数的图象如图：令t=f（x）则f（t）=m，
由图象可知：当t∈（-1，1）时，方程f（x）=t至多3个根，当t∉（-1，1）时，方程没有实数根，
而对于任意m∈R，方程f（t）=m至多有一个根，t∈（-1，1），
从而函数F（x）=f（f（x））-m的零点个数至多有3个．
故选：A．

点评 本题考查函数的单调性以及函数的奇偶性的应用，考查数形结合以及分类讨论思想的应用．