
 当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:
当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:| 及格(≥60) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
| P(K2≥K0) | 0.10 | 0.05 | 0.025 |
| K0 | 2.706 | 3.841 | 5.024 |
分析 (1)根据统计数据,可得2×2列联表,根据列联表中的数据,计算K2的值,即可得到结论;
(2)X的可能取值有0,1,2,求出相应的概率,可得X的分布列及数学期望.
解答 解:(1)由题意得列联表为:
| 及格(≥60) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
| X | 0 | 1 | 2 |
| P | (1-P1)(1-P2) | (1-P1)P2+P1(1-P2) | P1P2 |
点评 本题考查独立性检验,考查离散型随机变量的分布列与期望,考查学生的阅读与计算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
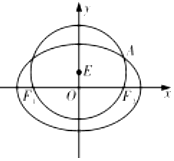 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 9个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
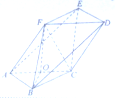 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
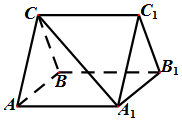 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com