
分析 (1)求函数的解析式,分类讨论解不等式|f(x)|+|f(-x)|≥6|x|;
(2)由题意可得,|f(x)-f(a)|=|x-a|•|x+a-2|<|x+a-2|.再根据|x+a-2|=|x-a+2a-2|≤|x-a|+|2a-2|,再利用条件以及绝对值不等式的性质证得结论.
解答 (1)解:由题意,b=2,$\frac{4c-{b}^{2}}{4}$=-1,∴c=0,
∴f(x)=x2-2x,
∴|f(x)|+|f(-x)|≥6|x|,即|x2-2x|+|x2+2x|≥6|x|,
∴x=0或|x-2|+|x+2|≥6,
x≤-2,不等式可化为-x+2-x-2≥6,∴x≤-3,∴x≤-3;
-2<x<2,不等式可化为-x+2+x+2≥6,不成立;
x≥2,不等式可化为x-2+x+2≥6,∴x≥3,∴x≥3,
综上所述,不等式的解集为{x|x≤-3或x≥3或x=0};
(2)证明:∵f(x)=x2-2x,∴|f(x)-f(a)|=|x2-2x-a2+2a|=|x-a|•|x+a-2|,
∵实数a满足|x-a|<1,∴|x-a|•|x+a-2|<|x+a-2|.
又|x+a-2|=|x-a+2a-2|≤|x-a|+|2a-2|<1+|2a-2|≤1+|2|a|+2=2|a|+3,
∴|f(x)-f(a)|<2|a|+3.
点评 本题主要考查二次函数的性质,考查不等式的解法,考查绝对值不等式的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 9个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=x2+1 | B. | f(x)=sinx | C. | f(x)=2x | D. | f(x)=log2|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
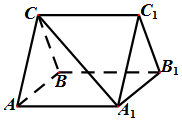 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
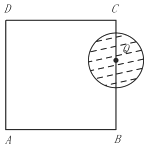 如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )| A. | $[{1-\frac{{\sqrt{2}}}{4},2+\frac{{\sqrt{2}}}{4}}]$ | B. | $[{\frac{3}{4},2+\frac{{\sqrt{2}}}{4}}]$ | C. | $[{\frac{3}{4},\frac{9}{4}}]$ | D. | $[{1-\frac{{\sqrt{2}}}{4},\frac{9}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ||MF1|-|MF2||>24 | B. | ||MF1|-|MF2||=24 | C. | ||MF1|-|MF2||<24 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com